A disc A of mass m sliding over a smooth horizontal surface with velocity v experiences a perfectly elastic collision with a smooth stationary wall at a point O (figure). The angle between the motion direction of the disc and the normal of the wall is equal to α. Find:
(a) the points relative to which the angular momentum M of the disc remains constant in this process,
(b) the magnitude of the increment of the vector of the disc's angular momentum relative to the point O′ which is located in the plane of the disc's motion at the distance l from the point O.
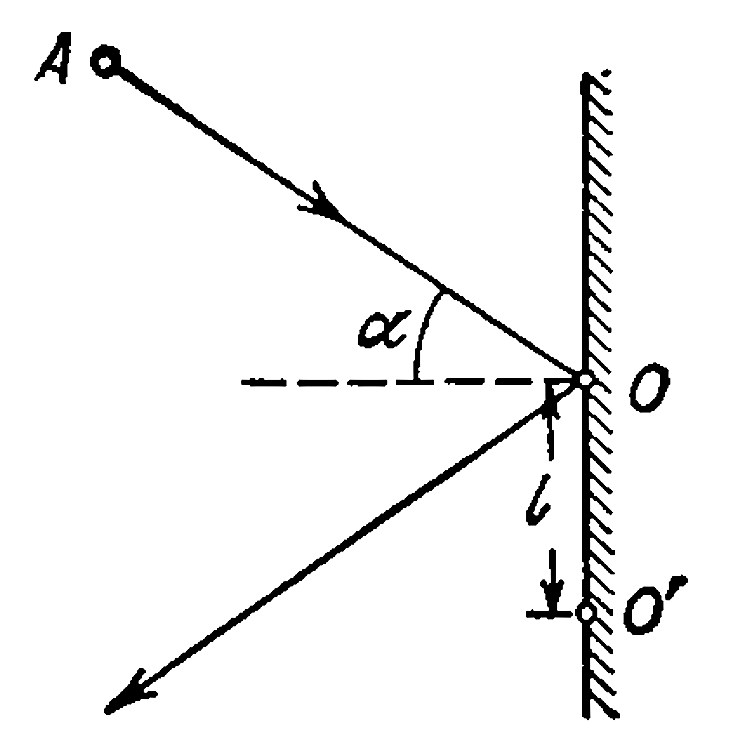
(a) The disc experiences gravity, the forces of reaction of the horizontal surface, and the force →R of reaction of the wall at the moment of the impact against it. The first two forces counter-balance each other, leaving only the force →R. It's moment relative to any point of the line along which the vector →R acts along normal to the wall is equal to zero and therefore the angular momentum of the disc relative to any of these points does not change in the given process.
(b) During the course of collision with wall the position of disc is same and is equal to →r∞′ Obviously the increment in linear momentum of the ball Δ→p=2mvcosαˆn
Here, Δ→M=→r∞′×Δ→p=2mvlcosαˆn and directed normally emerging from the plane of figure
Thus ∣∣Δ→M∣∣=2mvlcosα

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body56videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics59videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One

A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P isAzeroB45∘Ctan−1(2)Dtan−1(1/2) - Question 2 - Select One
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
 .AzeroB45∘C135∘Dtan−1(1/2)
.AzeroB45∘C135∘Dtan−1(1/2) - Question 3 - Select One
A disc of radius 0.1 mrolls without sliding on a horizontal suirface with a velocity of 6 m/s. It then ascends a smooth continous track as shown in figure. The height upto which it will ascend is (g=10m/s2)
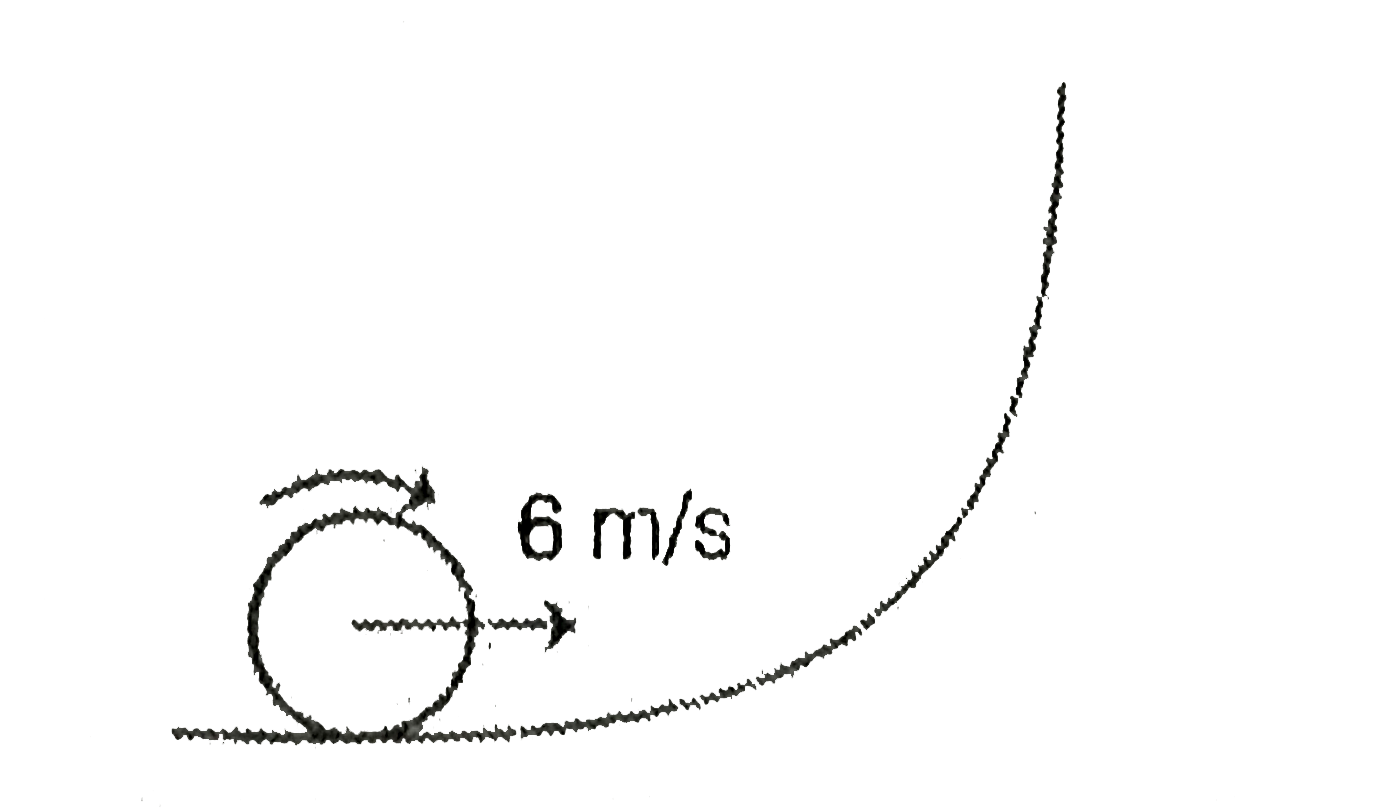 A2.4 mB0.9 mC2.7 mD1.8 m
A2.4 mB0.9 mC2.7 mD1.8 m
A uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
View SolutionA disc of radius 0.1 m rolls without sliding on a horizontal surface with a velocity of 6ms−1 . It then ascends a smooth continuous track as shown in figure. The height upto which it will ascend is (g=10ms−2)
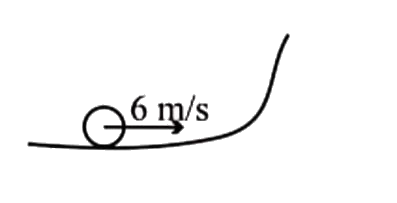 View Solution
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA smooth horizontal disc rotates with a constant angular velocity ω about a stationary vertical axis passing through its centre, the point O. At a moment t=0 a disc is set in motion from that:
point with velocity v0. Find the angular momentum M(t) of the disc relative to the point O in the reference frame fixed to the disc. Make sure that this angular momentum is caused by the Coriolis force.View Solution