A number of particles are projected from a given point with equal velocities in different directions in the same vertical plane. At any instant they will lie on
parabola
circle
hyperbola
rectangle
(b) Let a particle is projected at an angle θ with horizontal (shown in figure)
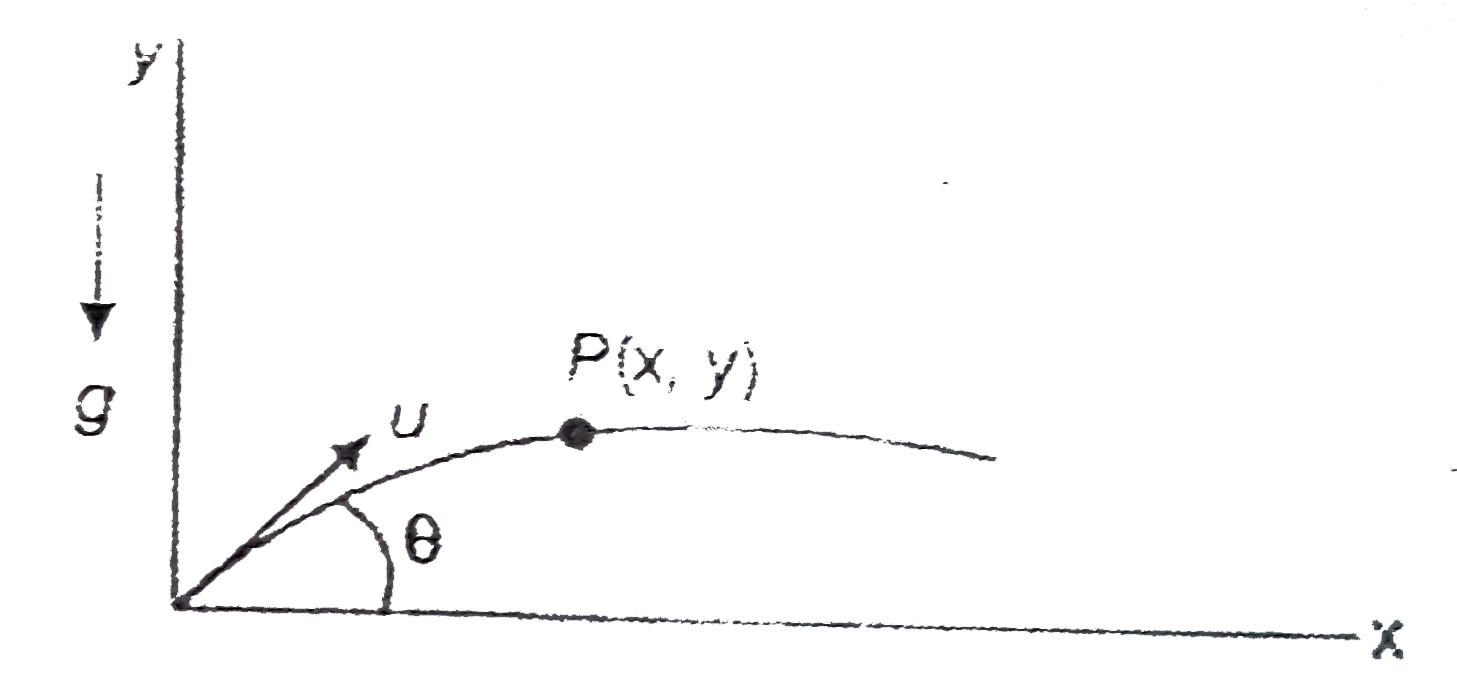
At an instant t, the particle reaches at point P(x,y).
∴X=(ucosθ)t
∴Utcosθ=x………..(i)
and y=(uyt)−12gt2
∴y=(usinθ)t−12gt2
∴utsinθ=y+12gt2..........(ii)
Squaring Eqs (i) and (ii) and then adding, we get
(utsinθ)2+(utcosθ)2=x2+(y+12gt2)2
∴u2t2=x2+y2+g2g44+gt2y
x2+y2+g2t44+gt2y−u2t2=0
Topper's Solved these Questions
Similar Questions
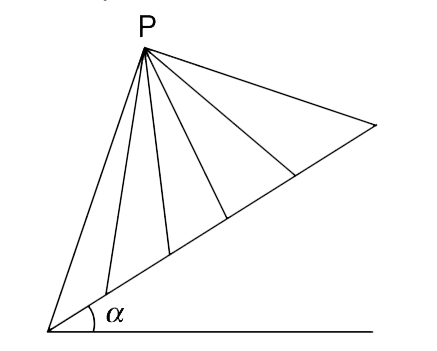
(a) Prove that bodies starting at the same time t=0 from the same point, and following frictionless slopes in different directions in the same vertical plane, all lie in a circle at any subsequent time.
(b) Using the above result do the following problem. A point P lies above an inclined plane of inclination angle α. P is joined to the plane at number of points by smooth wires, running in all possible directions. Small bodies (in shape of beads) are released from P along all the wires simultaneously. Which body will take least time to reach the plane.
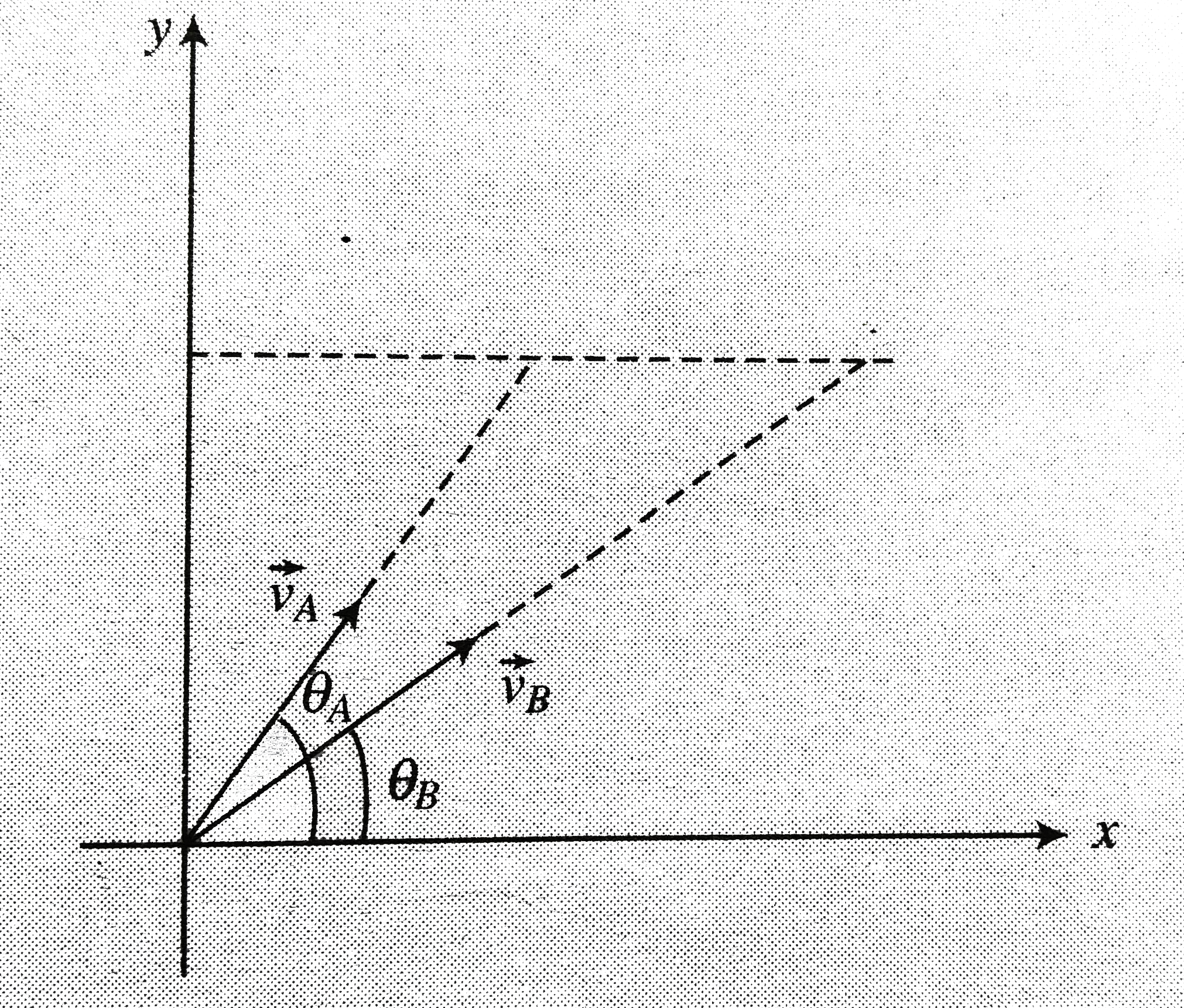
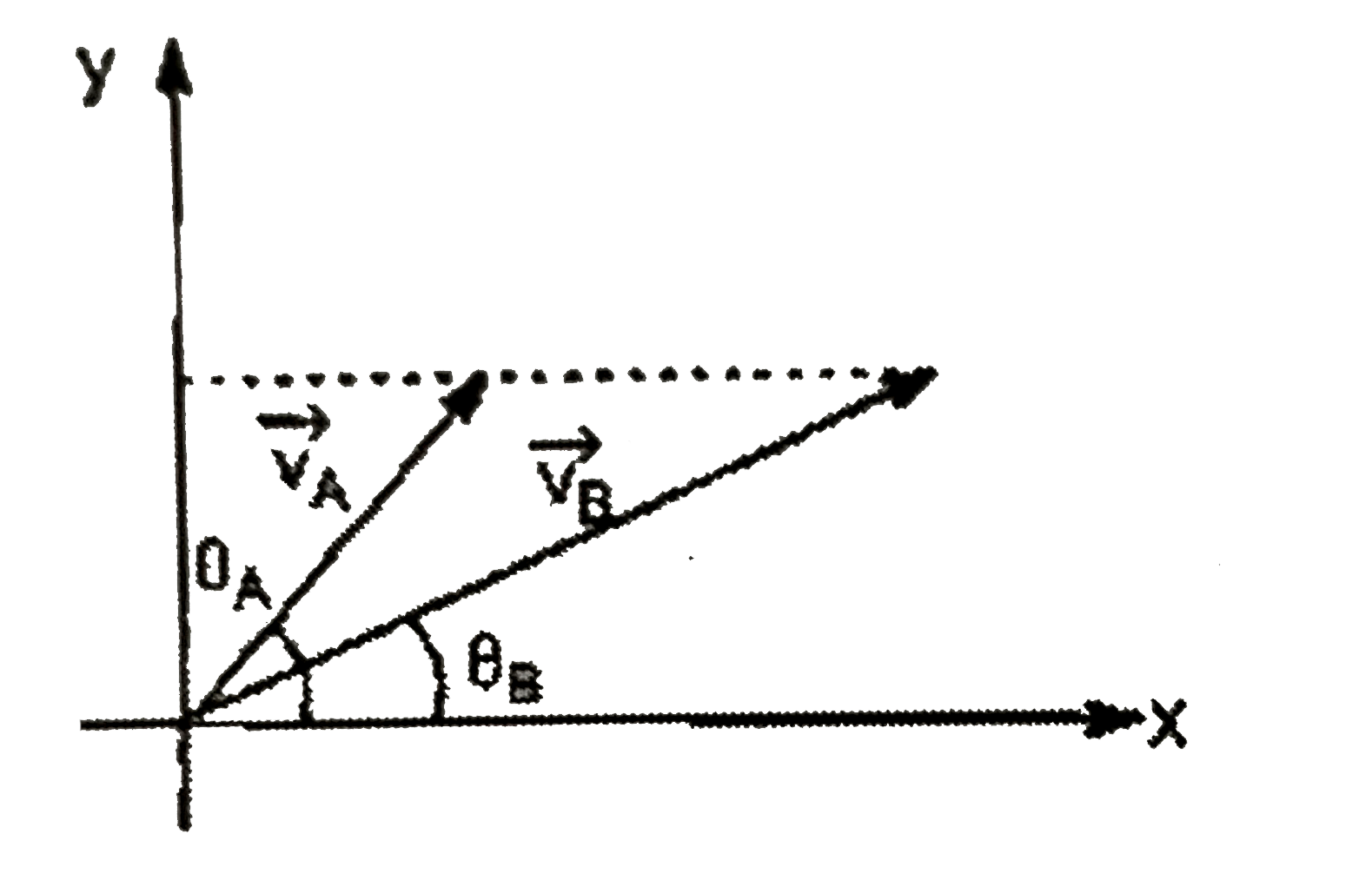
View SolutionTwo particles AandB are projected from the same point in different directions in such a manner that vertical components of their initial velocities are same (Fig. 5.8). Find the ratio of range.
 .
.
View Solution
Knowledge Check
Two bodies are projected from the same point with equal velocities in such a directions that they strike on the same point on a plane whose inclination is β. If α is the angle of projection of the first , the ration of there times of flight is
Asin(α−β):cosαBcosα:sin(α−β)Csinα+β:cosαDcosα:sin(α+β)Two particles are projected from the same point, with the same speed, in the same vertical plane, at different angles with the horizontal.A frame of references is fixed to one particle.The position vector of the other particle as observed from this frame is →rWhich of the following statements are corrects?
Adirection of →r does not changeB→r changes in magnitudes and direction with timeCThe magnitude of →r increases linearly with timeDThe direction of →r changes with time, its magnitude may or may not change, depending on the angles of projectionTwo identical particles 1 and 2 are projected from surface of earth with same velocities in the directions shows in figure.
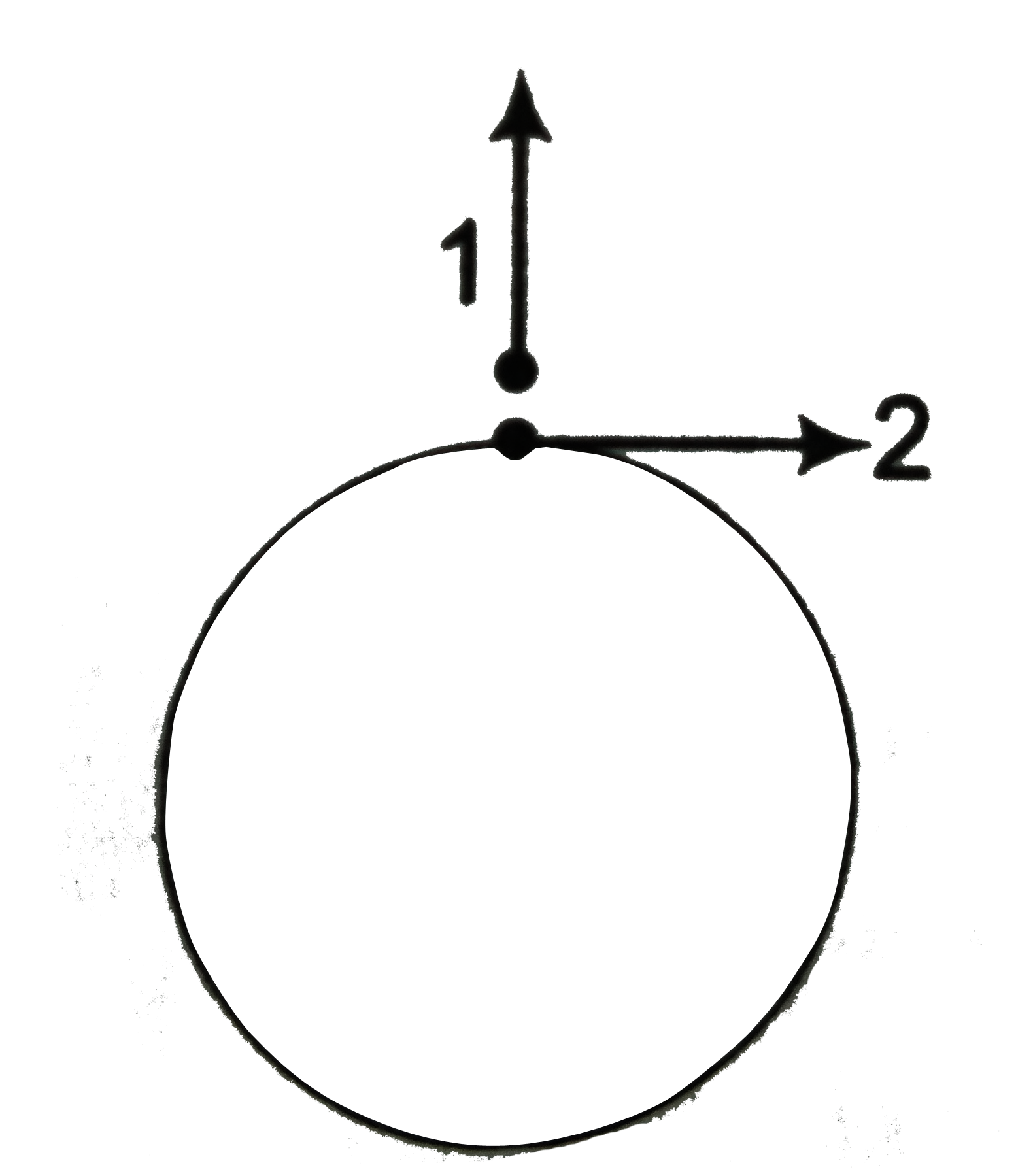 ABoth the particles will stop momentarily (before striking with ground)at different timesBParticle −1 will rise upto lesser height compared to particle−2CMinimum speed of particle−2 is more than that of particle−1DParticle −1 will strike the ground earlier
ABoth the particles will stop momentarily (before striking with ground)at different timesBParticle −1 will rise upto lesser height compared to particle−2CMinimum speed of particle−2 is more than that of particle−1DParticle −1 will strike the ground earlier
Iwo particles A & B are projected from the same point in, different directions in such a manner that vertical components of their initial velocities are same :
(a) Find ratio of time of flight
(b) Find ratio of range.
View SolutionA bomb is projected obliquely upward. It explodes at its highest point such that the pieces fly off with same speed in different directions in same vertical plane. Consider motion of the pieces of the bomb before they strike the ground
View SolutionTwo particles are projected simultaneously from the same point, with the same speed, in the same vertical plane, and at different angles with the horizontal in a uniform gravitational field acting vertically downwards. A frame of reference is fixed to one particle. The position vector of the other particle , as observed from this frame, is →r. Which of the following statement is correct?
View SolutionTwo particles A and B are projected from the same point in different direction in such a manner that their velocity vectors are shown in the diagram :−
 .
.
View SolutionA particle is projected from point A on the ground at an angle θ with horizontal. Another particle is projected from point B simultaneously from height 4H above point A with same velocity A and B are in the same vertical plane, where H is the maximum height attained by the particle A, Both the particle collide at the same time on the ground. Find the angle at which particle B is projected with hoizontal.
View Solution
