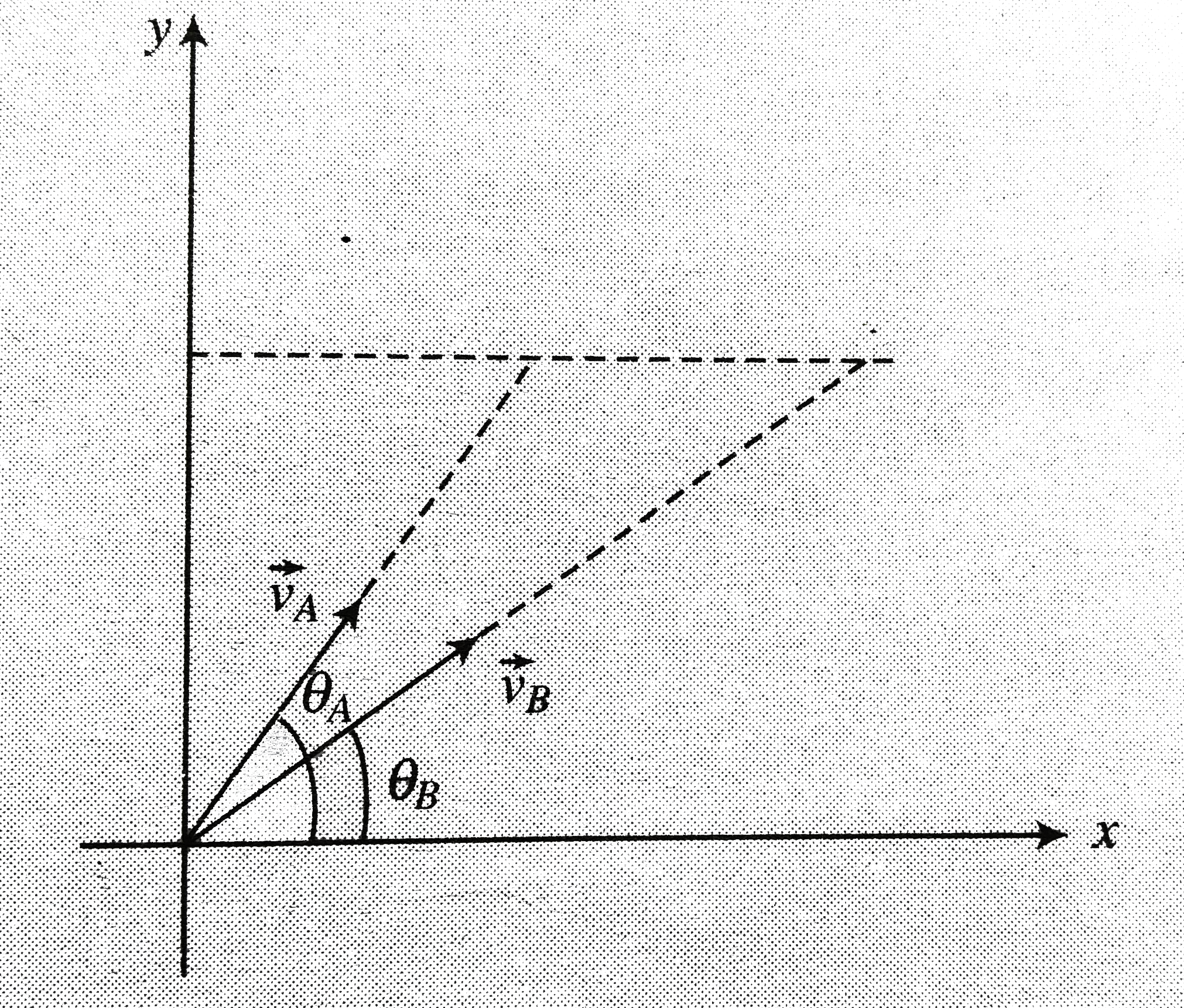
Two particles AandB are projected from the same point in different directions in such a manner that vertical components of their initial velocities are same (Fig. 5.8). Find the ratio of range.
 .
.
We know that the range of projectile,
R=u2sin2θg=(2usinθ)g×ucosθ=2ux.uyg
As (uy)1=(uy)2⇒uAsinθA=uBsinθB
or uAuB=sinθBsinθA
RARB=2(uAsinθA)(uAcosθA)/g2(uBsinθB)(uBcosθB)/g
=[uAcosθAuBcosθB]
=sinθBcosθAsinθAcosθB=tanθBtanθA.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples7videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.115videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
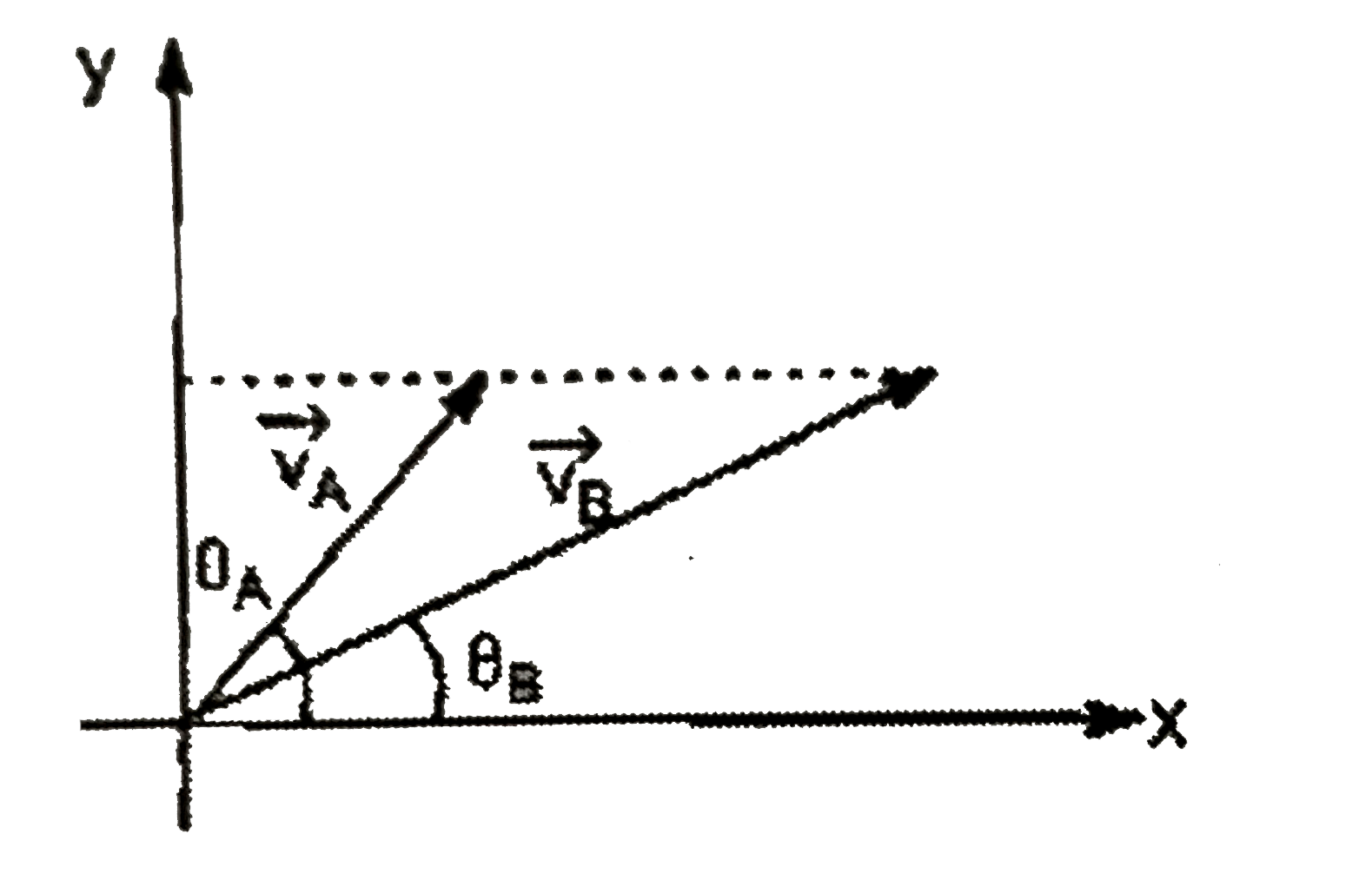
Iwo particles A & B are projected from the same point in, different directions in such a manner that vertical components of their initial velocities are same :
(a) Find ratio of time of flight
(b) Find ratio of range.
 View Solution
View SolutionTwo bodies are projected from the same point with same velocity but in different directions. If the range in each case be Rand the times of flight be t and t' then R=... in terms of t,t'
View Solution
Knowledge Check
- Question 1 - Select One
Two particles A and B are projected from the same point in different direction in such a manner that their velocity vectors are shown in the diagram :−
 .ATA=TBBTA>TBCTA<TBDCan't be determined
.ATA=TBBTA>TBCTA<TBDCan't be determined - Question 2 - Select One
A number of particles are projected from a given point with equal velocities in different directions in the same vertical plane. At any instant they will lie on
AparabolaBcircleChyperbolaDrectangle - Question 3 - Select One
Two projectiles thrown from the same point at angles 60∘and30∘ with the horizontal attain the same height. The ratio of their initial velocities is
A1B2C√3D1√3
Two particles P and Q are projected from two points in the same plane as shown. Find the condition for collision of two paricles.
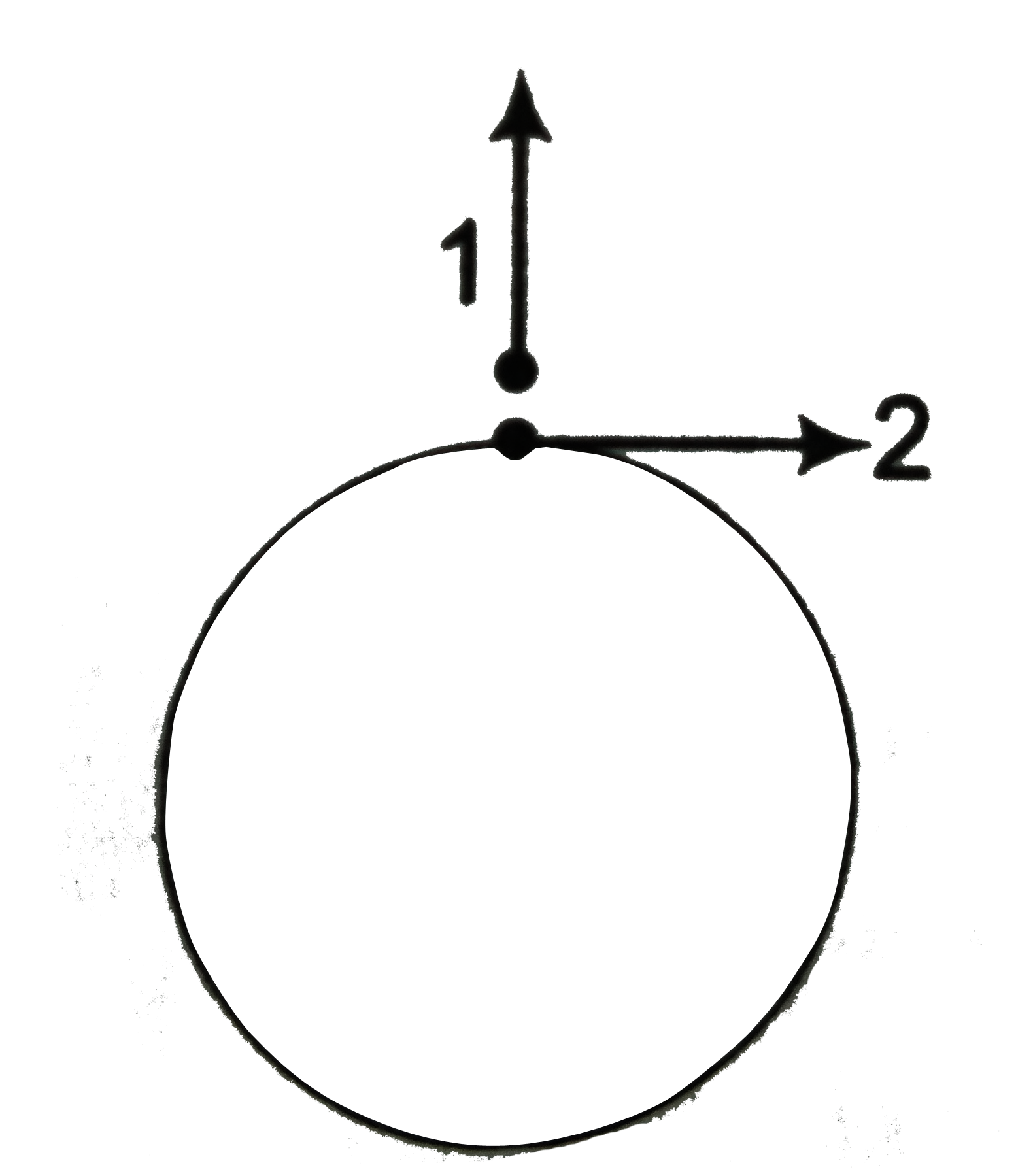
View SolutionTwo identical particles 1 and 2 are projected from surface of earth with same velocities in the directions shows in figure.
 View Solution
View SolutionTwo particles A and B are projected from the same point with the same velocity of projection but at different angles αand β of projection, such that the maximum height of A is two-third of the horizontal range of B. then which of the following relations are true?
View SolutionTwo particles A and B are projected from the same point with the same velocity of projection but at different angles αand β of projection, such that the maximum height of A is two-third of the horizontal range of B. then which of the following relations are true?
View SolutionTwo particle A and B projected along different directions from the same point P on the ground with the same velocity of 70 m/s in the same vertical plane. They hit the ground at the same point Q such that PQ = 480,. Then [g=9.8m/s2]
View Solution

