A object is thrown horizontally from a point A. The ball hits the ground at a point B. The line of sight from A to B makes 60° with the horizontal. If g = , the velocity of projection, if the time of flight is sec. is
The correct Answer is:B
To solve the problem step by step, we will analyze the motion of the object thrown horizontally from point A and hitting the ground at point B.
Step 1: Understanding the Problem
The object is thrown horizontally from point A and hits the ground at point B, making a line of sight at an angle of 60° with the horizontal. We are given the time of flight t=√3 seconds and the acceleration due to gravity g=10m/s2.
Step 2: Determine the Vertical Distance (y)
Using the equation of motion for vertical displacement:
y=ut+12at2
Since the object is thrown horizontally, the initial vertical velocity u=0. Thus, the equation simplifies to:
y=0+12(−g)t2
Substituting g=10m/s2 and t=√3:
y=12(−10)(√3)2=12(−10)⋅3=−15m
The negative sign indicates that the displacement is downward, so the vertical distance y=15m.
Step 3: Relate y and x using the Angle
From the geometry of the problem, we know that:
tan(60∘)=yx
Substituting the known value of y:
tan(60∘)=√3⇒√3=15x
Rearranging gives:
x=15√3=5√3m
Step 4: Calculate the Horizontal Velocity (v)
The horizontal distance x is covered in the time of flight t:
x=v⋅t
Substituting x=5√3 and t=√3:
5√3=v⋅√3
Dividing both sides by √3:
v=5m/s
Final Answer
The velocity of projection is 5m/s.
---
The object is thrown horizontally from point A and hits the ground at point B, making a line of sight at an angle of 60° with the horizontal. We are given the time of flight t=√3 seconds and the acceleration due to gravity g=10m/s2.
Using the equation of motion for vertical displacement:
y=ut+12at2
Since the object is thrown horizontally, the initial vertical velocity u=0. Thus, the equation simplifies to:
y=0+12(−g)t2
Substituting g=10m/s2 and t=√3:
y=12(−10)(√3)2=12(−10)⋅3=−15m
The negative sign indicates that the displacement is downward, so the vertical distance y=15m.
From the geometry of the problem, we know that:
tan(60∘)=yx
Substituting the known value of y:
tan(60∘)=√3⇒√3=15x
Rearranging gives:
x=15√3=5√3m
The horizontal distance x is covered in the time of flight t:
x=v⋅t
Substituting x=5√3 and t=√3:
5√3=v⋅√3
Dividing both sides by √3:
v=5m/s
The velocity of projection is 5m/s.
Similar Questions
A ball is thrown horizontally from a cliff such that it strikes the ground after 5s.The line of sight makes an angle 37∘ with the horizontal.The initial velocity of projection in ms−1 is
View SolutionA ball is projected horizontal from the top of a tower with a velocity v0. It will be moving at an angle of 60∘ with the horizontal after time.
View SolutionA ball is thrown from a point in level with velocity u and at a horizontal distance r from the top os a tower of height h.
At what horizontal distance x from the foot of the tower does the ball hit the ground ?
View SolutionA ball is thrown horizontally from a point 100m above the ground with a speed of 20m/s. Find (a) the time it takes to reach the ground, (b) the horizontal distance it travels before reaching the ground, (c) the velocity (direction and magnitude) with which it strikes the ground.
View SolutionA body is thrown horizontally from the top of a tower. It reaches the ground after 4s at an angle 45° to the ground. The velocity of projection is
View SolutionA javelin thrown into air at an angle with the horizontal has a range of 200 m. If the time of flight is 5 second, then the horizontal component of velocity of the projectile at the highest point of the trajectory is
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
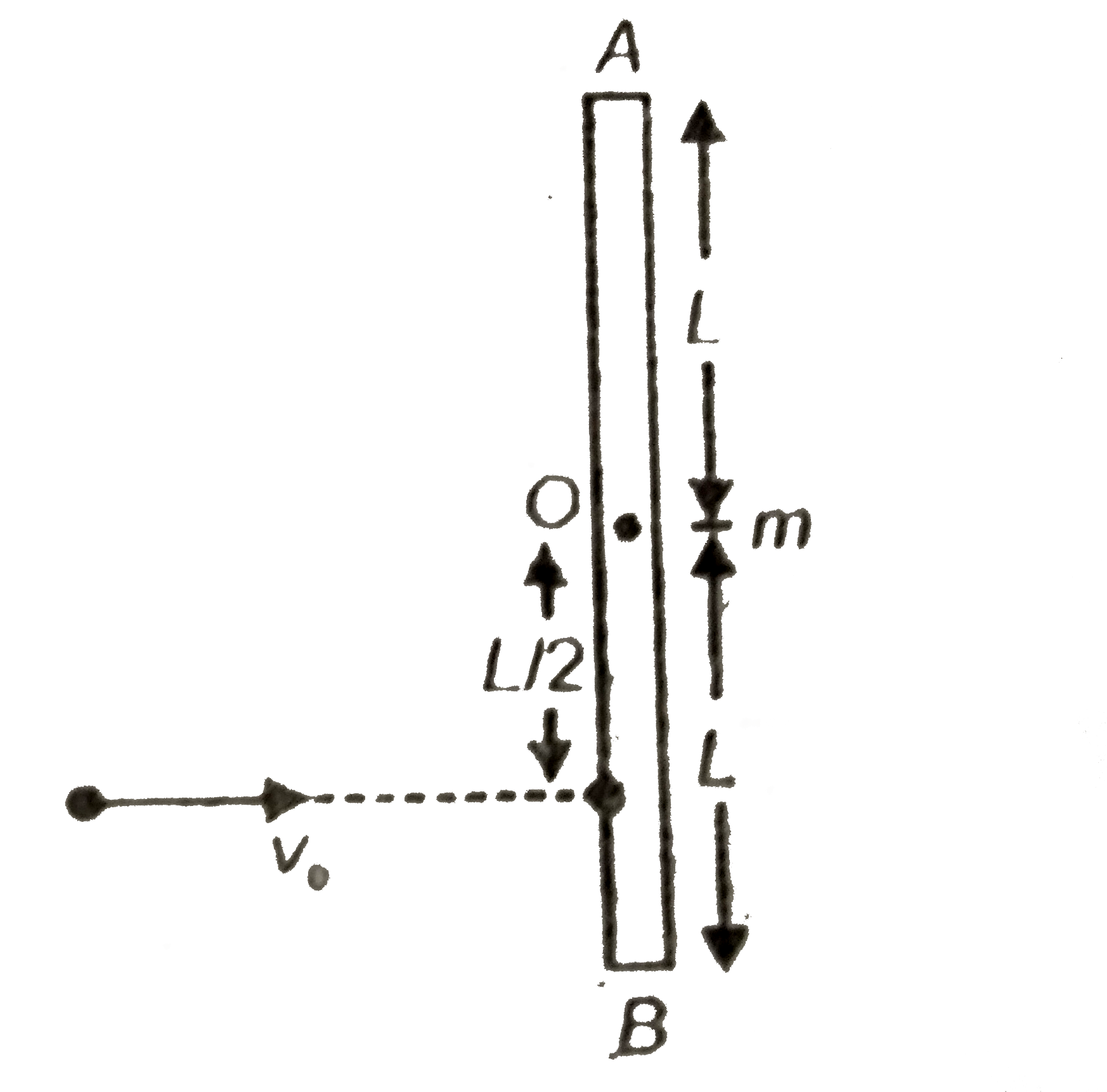
Distance of point P on rod from B which is at rest immediately afte collision is
View SolutionA particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
View SolutionA body is projected horizontally from the top of a tower with a velocity of 30 m/s. The velocity of the body 4 seconds after projection is (g = 10ms−2)
View SolutionA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View Solution
