From the top of a tower 20m high, a ball is thrown horizontally. If the line joining the point of projection to the point where it hits the ground makes an angle of 45∘ with the horizontal, then the initial velocity of the ball is:
10ms−1
4ms−1
15ms−1
3ms−1
The correct Answer is:a
To solve the problem, we need to analyze the motion of the ball thrown horizontally from the top of a tower. The tower is 20 meters high, and we know that the line joining the point of projection to the point where it hits the ground makes an angle of 45 degrees with the horizontal.
Step 1: Understand the Geometry of the Problem
When the ball is thrown horizontally from a height of 20 meters, it will fall under the influence of gravity while moving horizontally. The trajectory of the ball will form a right triangle where:
- The vertical side (height of the tower) is 20 m.
- The horizontal side is the horizontal distance (range) traveled by the ball before it hits the ground.
- The hypotenuse is the line joining the point of projection to the point where it hits the ground, which makes a 45-degree angle with the horizontal.
Step 2: Use the Properties of the Triangle
Since the angle is 45 degrees, the horizontal distance (let's denote it as R) and the height (20 m) must be equal because in a 45-degree right triangle, the two legs are equal. Thus:
R=20m
Step 3: Calculate the Time of Flight
The time t it takes for the ball to fall 20 m can be calculated using the formula for free fall:
h=12gt2
where h=20m and g=9.81m/s2.
Rearranging the formula to solve for t:
20=12×9.81×t2
t2=20×29.81
t2=409.81
t=√409.81
t≈2.02s
Step 4: Calculate the Initial Velocity
The horizontal distance R traveled by the ball can also be expressed in terms of the initial horizontal velocity u and the time of flight t:
R=u⋅t
Substituting the values we have:
20=u⋅2.02
u=202.02
u≈9.90m/s
Final Answer
The initial velocity of the ball is approximately 9.90m/s.
---
When the ball is thrown horizontally from a height of 20 meters, it will fall under the influence of gravity while moving horizontally. The trajectory of the ball will form a right triangle where:
- The vertical side (height of the tower) is 20 m.
- The horizontal side is the horizontal distance (range) traveled by the ball before it hits the ground.
- The hypotenuse is the line joining the point of projection to the point where it hits the ground, which makes a 45-degree angle with the horizontal.
Since the angle is 45 degrees, the horizontal distance (let's denote it as R) and the height (20 m) must be equal because in a 45-degree right triangle, the two legs are equal. Thus:
R=20m
The time t it takes for the ball to fall 20 m can be calculated using the formula for free fall:
h=12gt2
where h=20m and g=9.81m/s2.
20=12×9.81×t2
t2=20×29.81
t2=409.81
t=√409.81
t≈2.02s
The horizontal distance R traveled by the ball can also be expressed in terms of the initial horizontal velocity u and the time of flight t:
R=u⋅t
Substituting the values we have:
20=u⋅2.02
u=202.02
u≈9.90m/s
The initial velocity of the ball is approximately 9.90m/s.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Projection From Inclined Plane20videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Relative Velocity In Two Dimensions23videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test29videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration15videos
MOCK TEST
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
Similar Questions
From the top of a building 19.6 m high, a ball is projected horizontal. After how long does it strike the ground ? If the line joining the point of projection to the point where it hits the ground makes an angle of 45∘ with the horizontal, what is the initial velocity of the ball ?
View SolutionA boy kicks a football horizontally from the roof of a building of height 10m, . If the line joining the initial position of the football and the point where it hits the ground make an angle of 45∘ with the ground, then find the displacement of the football
View Solution
Knowledge Check
- Question 1 - Select One
From the the top of a tower 19.6 m high, a ball is thrown horizontally. If the line joining the point of projection to the point where it hits the ground makes an angle of 45∘ with the horizontal, then the initial velocity of the ball is:-
A9.8ms−1B4.9ms−1C14.7ms−1D2.8ms−1 - Question 2 - Select One
From the top of a building 80mhigh, a ball is thrown horizontally which hits the ground at a distance.The line joining the top of the building to the point where it hits the ground makes an angle of 45∘ with the ground. Initial velocity of projection of the ball is (g=10m/s2)
A10m/sB15m/sC20m/sD30m/s - Question 3 - Select One
A ball is thrown horizontally from a cliff such that it strikes the ground after 5s.The line of sight makes an angle 37∘ with the horizontal.The initial velocity of projection in ms−1 is
A50B100√3C100√2D1003
A boy kicks a football horizontally from the roof of a building of height 10m, . If the line joining the initial position of the football and the point where it hits the ground make an angle of 45∘ with the ground, then find the displacement of the football
View SolutionAn object is projected horizontally from a top of the tower of height h.The line joining the point of projection and point of striking on the ground makes an angle 45∘ with ground,Then with what velocity the object strikes the ground
View SolutionAn object is thrown from a point 'A' horizontally from a tower and hits the ground 3s later at B. The line from 'A' to 'B' makes an angle of 30∘ with the horizontal. The initial velocity of the object is 15√xm/s. Find x : (take g=10m/s2)
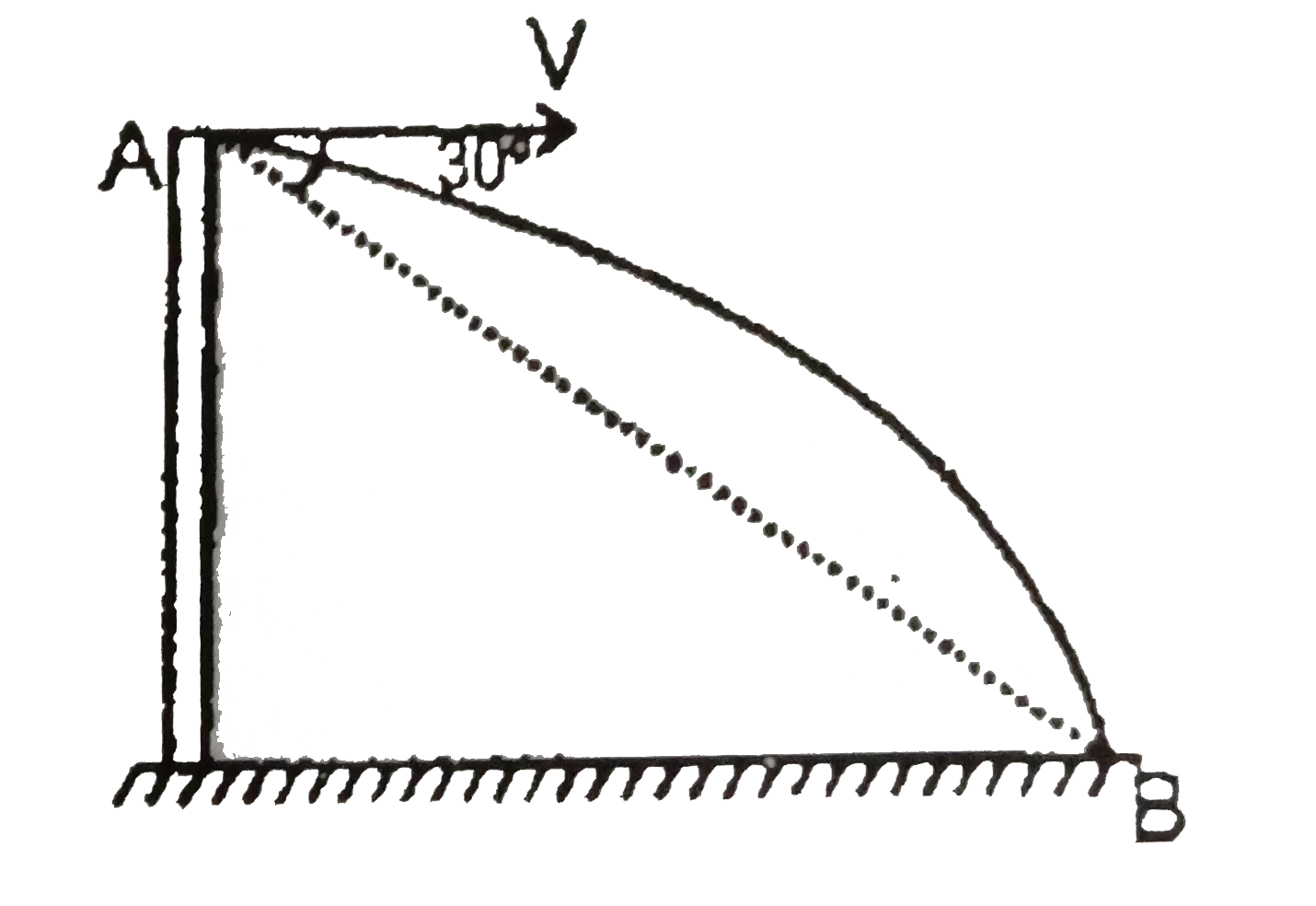 View Solution
View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
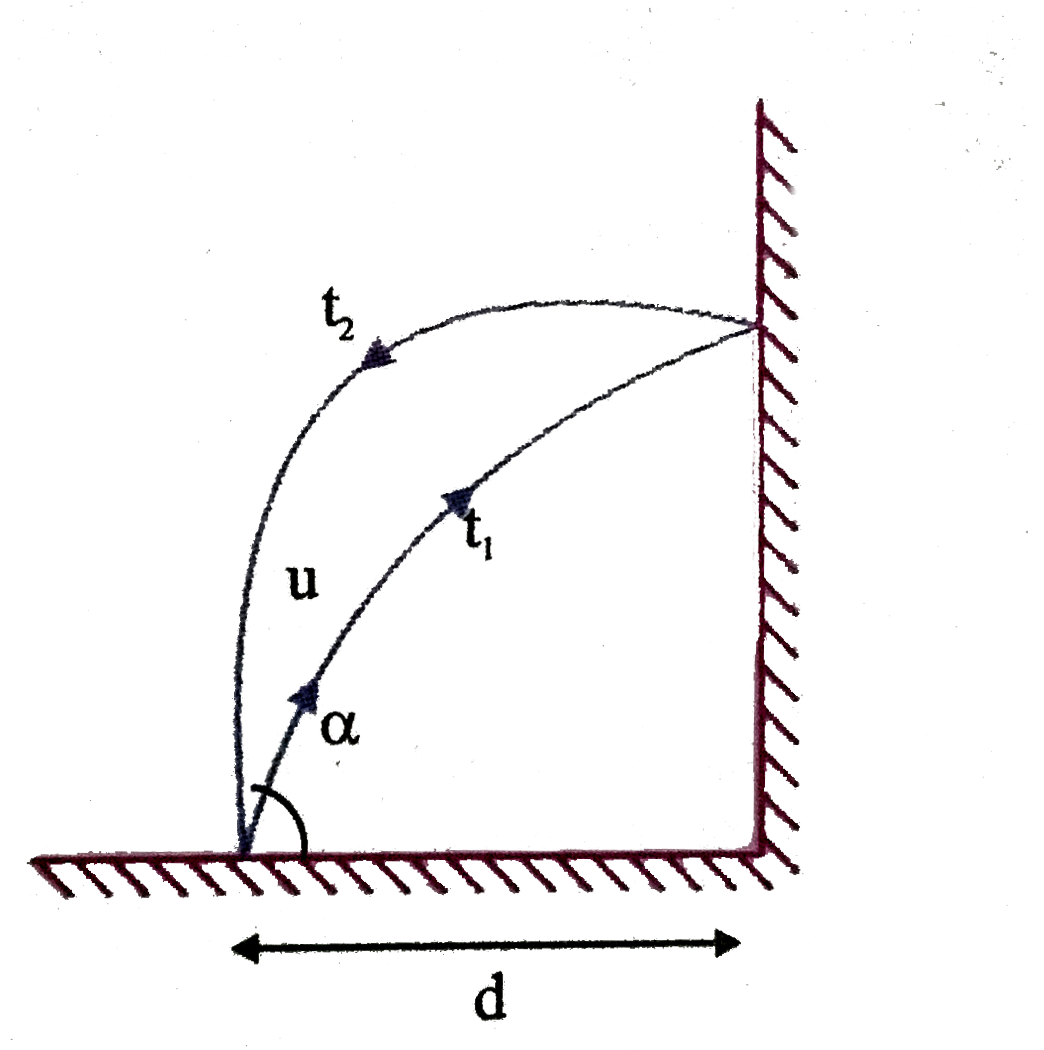
If the line joining the point of projection and the point of impact makes an angle 'θ' with the horizontal, then tanθ isView SolutionA body is thrown horizontally from the top of a tower. It reaches the ground after 4s at an angle 45∘ to the ground. The velocity of projection is
View Solution

