(a) Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid. (b) How does this magnetic energy compare with the electrostatic energy stored in a capacitor?
(a) From Eq. (6.19), the magnetic energy is
UB=12LI2
=12L(Bμ0n)2 (since B=μ0ni, for a solenoid)
12(μ0n2Al)(Bμ0n)2 [From Eq. (6.17)]
=12μ0B2Al
(b) The magnetic energy per unit volume is,
ub=UBV (where V is volume that contains flux)
=UBAl
=B22μ0
We have already obtained the relation for the electrostatic energy stored per unit volume in a parallel plate capacitor (refer to Chapter 2, Eq. 2.77),
uE=12ε0E2
In both the cases energy is proportional to the square of the field strength. Equations (6.20) and (2.77) have been derived for special cases: a solenoid and a parallel plate capacitor, respectively. But they are general and valid for any region of space in which a magnetic field or/and an electric field exist.
Topper's Solved these Questions
Similar Questions
(a) Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid. (b) How does this magnetic energy compare with the electrostatic energy stored in a capacitor?
View Solution(a) Obtain the expression for the magnetic energy stored in a solenoid, due to the current I flowing in it, in terms of magnetic field B, area of cross-section A and length l of the solenoid.
(b) How is this magnetic energy per unit volume compared with the electrostatic energy per unit volume stored in a parallel plate capacitor ?View Solution
Knowledge Check
- Question 1 - Select One
In the figure magnetic energy stored in the coil is
 AzeroBinfiniteC25 joulesDnone of the above
AzeroBinfiniteC25 joulesDnone of the above - Question 2 - Select One
Magnetic field energy stored in a coil is
ALi2B12LiCLiD12Li2
The total electrostatic energy stored in both the capacitor is
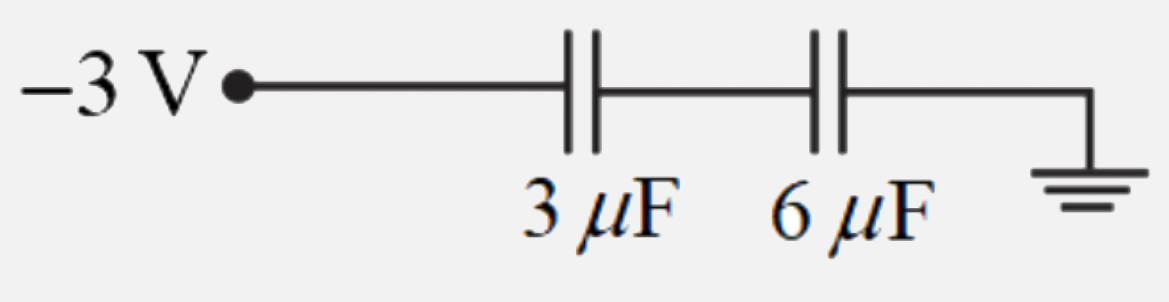 View Solution
View SolutionMagnetic energy stored per unit volume in a magnetic field is _____.
View SolutionWhat is expression for magnetic energy stored in an inductor. Compare it with the electrostatic energy stored in a capacitor.
View SolutionStarting from the expression for the energy W=1/2LI2, stored in a solenoid of self-inductance L to build up the current I, obtain the expression for the magnetic energy in terms of the magnetic field B, area A and length l of the solenoid having n number of turns per unit length. Hence, show that the energy density is given by B2/2μ0.
View SolutionHow does the magnetic length of a magnet compare to the geometric length of a magnet?
View SolutionThe total electrostatic energy stored in both the capacitors (in μJ) is
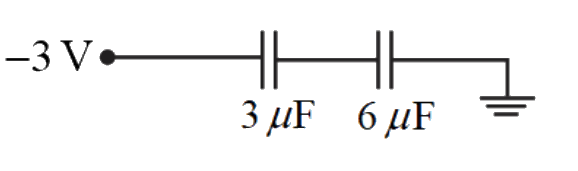 View Solution
View Solution

