A parallel beam of white light is incident on a thin film of air of uniform thickness. Wavlength 7200Å and 5400Å are observed to be missing from the spectrum of reflected light viewed normally. The other wavelength in the visible region missing in the reflected spectrum is
6000Å
4320Å
5500Å
6500Å
The correct Answer is:b
To solve the problem, we need to find the third missing wavelength in the reflected spectrum when white light is incident on a thin film of air. The wavelengths given are 7200 Å and 5400 Å. Let's go through the solution step by step.
Step 1: Understanding the Condition for Destructive Interference
In a thin film, destructive interference occurs when the path difference between the light reflected from the top and bottom surfaces of the film leads to a phase difference of an odd multiple of π (or half a wavelength). The condition for destructive interference can be expressed as:
2μt=nλ
where:
- μ is the refractive index of the film (for air, μ≈1),
- t is the thickness of the film,
- n is an integer (order of interference),
- λ is the wavelength of light.
Step 2: Setting Up the Equations
Given that two wavelengths are missing (7200 Å and 5400 Å), we can set up the equations for these wavelengths:
1. For λ1=7200Å:
2μt=n⋅7200
2. For λ2=5400Å:
2μt=(n+1)⋅5400
Step 3: Equating the Two Expressions
Since both expressions equal 2μt, we can set them equal to each other:
n⋅7200=(n+1)⋅5400
Step 4: Solving for n
Expanding the equation:
n⋅7200=n⋅5400+5400
Rearranging gives:
n⋅7200−n⋅5400=5400
Factoring out n:
n(7200−5400)=5400
n⋅1800=5400
Thus,
n=54001800=3
Step 5: Finding the Third Wavelength
Now that we have n=3, we can find the third wavelength λ3 that will also be missing:
Using the condition for the third wavelength:
2μt=(n+2)⋅λ3
Substituting n=3:
2μt=5⋅λ3
From the first equation (for n=3):
2μt=3⋅7200
Setting the two equations equal gives:
3⋅7200=5⋅λ3
Solving for λ3:
λ3=3⋅72005=216005=4320Å
Conclusion
The other wavelength in the visible region that is missing in the reflected spectrum is 4320 Å.
---
In a thin film, destructive interference occurs when the path difference between the light reflected from the top and bottom surfaces of the film leads to a phase difference of an odd multiple of π (or half a wavelength). The condition for destructive interference can be expressed as:
2μt=nλ
where:
- μ is the refractive index of the film (for air, μ≈1),
- t is the thickness of the film,
- n is an integer (order of interference),
- λ is the wavelength of light.
Given that two wavelengths are missing (7200 Å and 5400 Å), we can set up the equations for these wavelengths:
1. For λ1=7200Å:
2μt=n⋅7200
2. For λ2=5400Å:
2μt=(n+1)⋅5400
Since both expressions equal 2μt, we can set them equal to each other:
n⋅7200=(n+1)⋅5400
Expanding the equation:
n⋅7200=n⋅5400+5400
Rearranging gives:
n⋅7200−n⋅5400=5400
Factoring out n:
n(7200−5400)=5400
n⋅1800=5400
Thus,
n=54001800=3
Now that we have n=3, we can find the third wavelength λ3 that will also be missing:
Using the condition for the third wavelength:
2μt=(n+2)⋅λ3
Substituting n=3:
2μt=5⋅λ3
2μt=3⋅7200
Setting the two equations equal gives:
3⋅7200=5⋅λ3
Solving for λ3:
λ3=3⋅72005=216005=4320Å
The other wavelength in the visible region that is missing in the reflected spectrum is 4320 Å.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct8videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective11videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
When white light is incident normally an oil film of thickness 10−4cm and refractive index. 1.4 then the wavelength which will not be seen in the reflected system of light is
View SolutionA parallel beam of white light is incident normally on a water film1.0x10−4 cm thick. Find the wavelength in the visible range (400 nm-700 nm) which are strongly transmitted by the film Refractive index of water = 1.33.
View SolutionA parallel beam of white light falls on a thin film whose refractive index is equal to 4/3. The angle of incidence i=53∘. What must be the minimum film thickness if the reflected light is to be coloured yellow most intensively? (tan53∘=4/3)
View SolutionRefractive index of a thin soap film of a uniform thickness is 1.38. The smallest thickness of the film that gives an interference maxima in the reflected light when light of wavelength 5520 Å falls at normal incidence is
View SolutionRefractive index of a thin soap film of a uniform thickness is 1.34. Find the smallest thickness of the film that gives in interference maximum in the reflected light when light of wavelength 5360Å fall at normal incidence.
View SolutionA thin film of refractive index 1.5 and thickness 4×10−5 cm is illuminated by light normal to the surface. What wavelength within the visible spectrum will be intensified in the reflected beam?
View SolutionA beam of white light is incident on the glass-air interface from glass to air such that green light just suffers total internal reflection. The colors of the light which will come out to air are
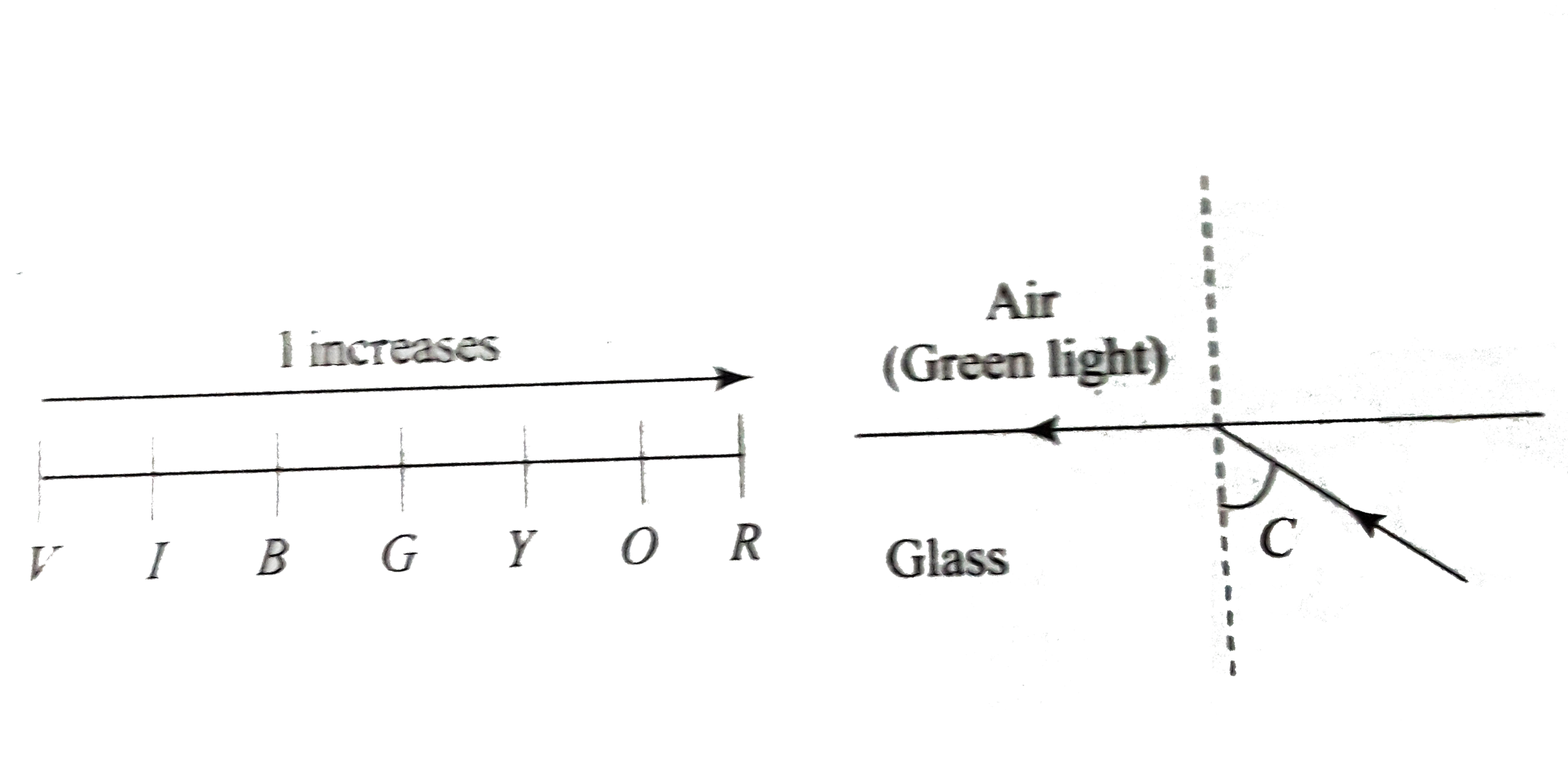 View Solution
View SolutionWhite light is incident normally on a glass plate (in air) of thickness 500nm and refractive index of 1.5. The wavelength (in nm) in the visible region (400nm−700nm) that is strongly reflected by the plate is:
View SolutionA glass plate (n=1.53) that is 0.485 μ m thick and surrounded by air is illuminated by a beam of white light normal to the plate.
(a) What wavelengths (in air) within the limits of the visible spectrum (λ=400to700nm) are intensified in the reflected beam ?
(b) What wavelengths within the visible spectrum are intensified in the transmitted light?View SolutionTwo thin films of the same material but different thickness are separated by air. Monochormatic light is incident on the first film. When viewed normally form point A, the second film appears dark.
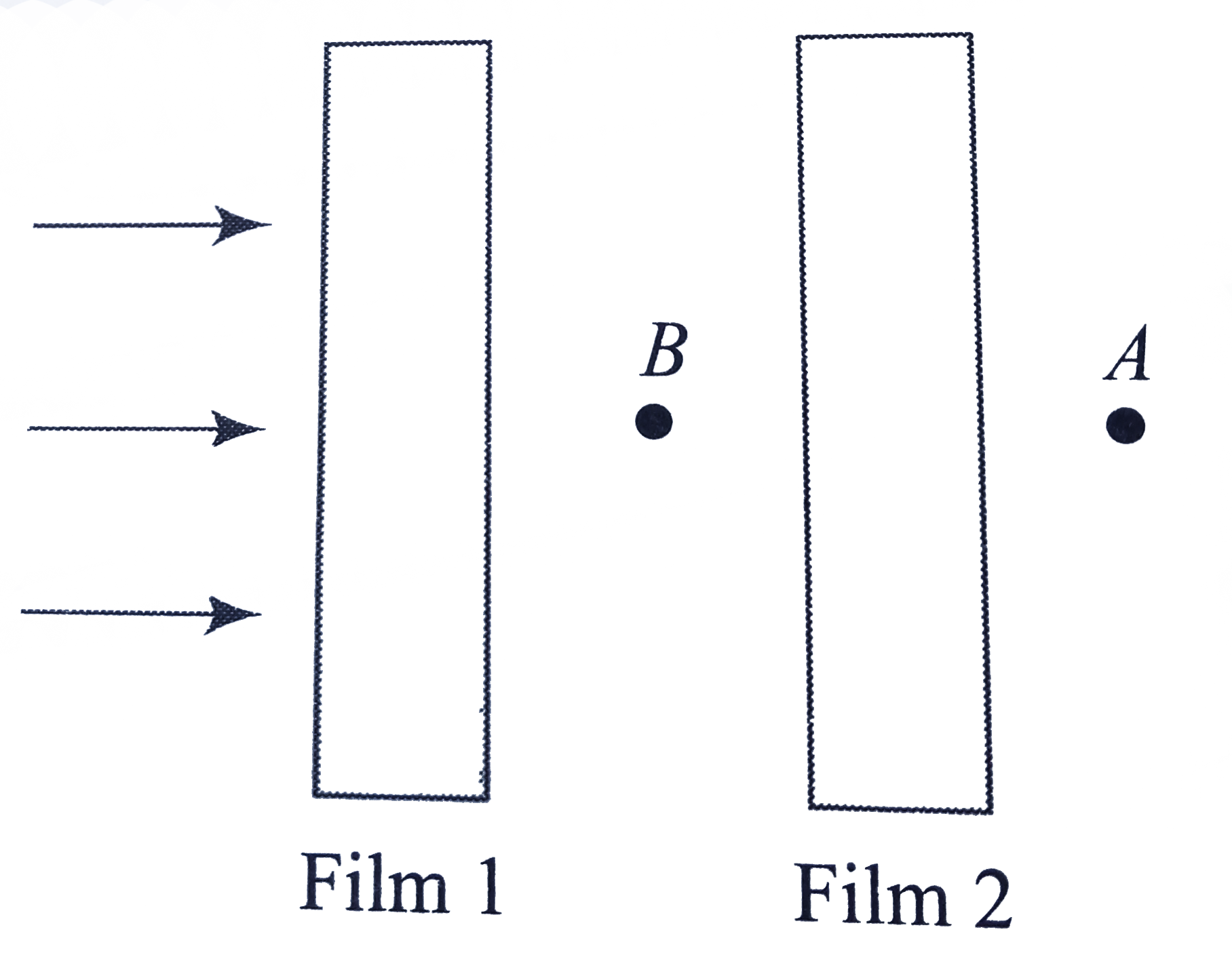 View Solution
View Solution

