A parallel plate capacitor has a uniform electric field →E in the space between the plates. If the distance between the plates is 'd' and the area of each plate is 'A' the energy stored in the capacitor is
ε0E2Ad2
E2Adε0
ε0E22
(ε0EAd)
To find the energy stored in a parallel plate capacitor with a uniform electric field →E, we can follow these steps:
Step 1: Understand the parameters
We have a parallel plate capacitor with:
- Distance between the plates: d
- Area of each plate: A
- Uniform electric field between the plates: E
Step 2: Recall the formula for energy stored in a capacitor
The energy U stored in a capacitor can be expressed using the formula:
U=12CV2
where C is the capacitance and V is the potential difference across the plates.
Step 3: Find the capacitance C
For a parallel plate capacitor, the capacitance C is given by:
C=ϵ0Ad
where ϵ0 is the permittivity of free space.
Step 4: Relate potential difference V to electric field E
The potential difference V across the plates can be related to the electric field E and the distance d as follows:
V=E⋅d
Step 5: Substitute C and V into the energy formula
Now, substituting the expressions for C and V into the energy formula:
U=12(ϵ0Ad)(E⋅d)2
Step 6: Simplify the expression
Substituting V=E⋅d into the equation gives:
U=12(ϵ0Ad)(E2⋅d2)
Now, simplify this expression:
U=12ϵ0AE2d2d
U=12ϵ0AE2d
Final Result
Thus, the energy stored in the capacitor is:
U=12ϵ0AE2d
We have a parallel plate capacitor with:
- Distance between the plates: d
- Area of each plate: A
- Uniform electric field between the plates: E
The energy U stored in a capacitor can be expressed using the formula:
U=12CV2
where C is the capacitance and V is the potential difference across the plates.
For a parallel plate capacitor, the capacitance C is given by:
C=ϵ0Ad
where ϵ0 is the permittivity of free space.
The potential difference V across the plates can be related to the electric field E and the distance d as follows:
V=E⋅d
Now, substituting the expressions for C and V into the energy formula:
U=12(ϵ0Ad)(E⋅d)2
Substituting V=E⋅d into the equation gives:
U=12(ϵ0Ad)(E2⋅d2)
Now, simplify this expression:
U=12ϵ0AE2d2d
U=12ϵ0AE2d
Thus, the energy stored in the capacitor is:
U=12ϵ0AE2d
Topper's Solved these Questions
Similar Questions
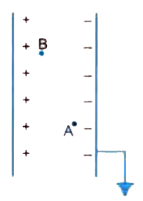
In a parallel plate capacitor the potential difference of 100 V is manitianed between the plates. If distance between the plates be 5mm, what will be the electric field at points A and B ?
View SolutionA parallel plate capacitor has an electric field of 105V/m between the plates. If the charge on the capacitor plate is 1μC, the force on each capacitor plate is
View Solution
Knowledge Check
A parallel plate capacitor has a uniform electric field E in the space between the the plates. If the distance between the plates is d and area of each plate is A, the energy stored in the capacitor is
A12ε0E2BE2Adε0C12ε0E2AdDeisi0E2AdA parallel plate capacitor has a uniform electric field E in the space between the plates. If the distance between the plates is ‘d and area of each plate is ‘A’, the energy stored in the capacitor is
A12ε0E2AdBE2Adε0C12ε0E2Dε0E.AdA parallel plate condenser has a unifrom electric field E(V/m) in the space between the plates. If the distance between the plates is d(m) and area of each plate is A(m2) the energy (joule) stored in the condenser is
A12ε0E2Bε0EAdC12ε0E2AdDE2Ad∣ε0
A parallel plate capacitor has an electric field of 105V/m between the plates. If the charge on the capacitor plate is 1μC, then force on each capacitor plate is-
View SolutionThe capacity of a parallel plate capacitor is 10μF, when the distance between its plates is 8 cm. If the distance between the plates is reduced to 4 cm, the new capacity of the parallel plate capacitor will be
View SolutionAs the distance between the plates of a parallel plate capacitor decreased
View SolutionIf the separation between the plates of a capacitor is 5 mm , then area of the plate of a 3 F parallel plate capacitor is
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View Solution
