A parallel plate capacitor has plate area 100 and plate separation of 10 m. The space between the plates is filled up to a thickness 5 m with a material of dielectric constant of 10. The resultant capacitance of the system is 'x' . The value of
The value of 'x' to the nearest integer is____________.
To solve the problem, we need to find the resultant capacitance of a parallel plate capacitor with a dielectric material partially filling the space between the plates.
Given Data:
- Plate area, A=100m2
- Plate separation, d=10m
- Thickness of dielectric, d1=5m
- Dielectric constant, K=10
- Permittivity of free space, ϵ0=8.85×10−12F/m
Step 1: Calculate the capacitance of the section with the dielectric.
The capacitance C1 of the section filled with the dielectric can be calculated using the formula:
C1=K⋅ϵ0⋅Ad1
Substituting the known values:
C1=10⋅(8.85×10−12)⋅1005
Calculating this gives:
C1=10⋅8.85×10−105=1.77×10−9F
Step 2: Calculate the capacitance of the section filled with air.
The remaining space between the plates (which is air) has a thickness of:
d2=d−d1=10−5=5m
The capacitance C2 of the air-filled section is given by:
C2=ϵ0⋅Ad2
Substituting the known values:
C2=(8.85×10−12)⋅1005
Calculating this gives:
C2=8.85×10−105=1.77×10−10F
Step 3: Combine the capacitances in series.
Since the two sections are in series, the total capacitance C can be calculated using the formula for capacitors in series:
1C=1C1+1C2
Substituting the values:
1C=11.77×10−9+11.77×10−10
Calculating the reciprocals:
1C=0.565+5.65=6.215
Thus,
C=16.215≈0.161×10−9F=1.61×10−10F
Step 4: Convert to picoFarads.
To convert to picoFarads:
C=1.61×10−10F=161pF
Final Step: Round to the nearest integer.
The value of x to the nearest integer is:
161
- Plate area, A=100m2
- Plate separation, d=10m
- Thickness of dielectric, d1=5m
- Dielectric constant, K=10
- Permittivity of free space, ϵ0=8.85×10−12F/m
The capacitance C1 of the section filled with the dielectric can be calculated using the formula:
C1=K⋅ϵ0⋅Ad1
Substituting the known values:
C1=10⋅(8.85×10−12)⋅1005
Calculating this gives:
C1=10⋅8.85×10−105=1.77×10−9F
The remaining space between the plates (which is air) has a thickness of:
d2=d−d1=10−5=5m
The capacitance C2 of the air-filled section is given by:
C2=ϵ0⋅Ad2
Substituting the known values:
C2=(8.85×10−12)⋅1005
Calculating this gives:
C2=8.85×10−105=1.77×10−10F
Since the two sections are in series, the total capacitance C can be calculated using the formula for capacitors in series:
1C=1C1+1C2
Substituting the values:
1C=11.77×10−9+11.77×10−10
Calculating the reciprocals:
1C=0.565+5.65=6.215
Thus,
C=16.215≈0.161×10−9F=1.61×10−10F
To convert to picoFarads:
C=1.61×10−10F=161pF
The value of x to the nearest integer is:
161
Topper's Solved these Questions
Similar Questions
Two parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
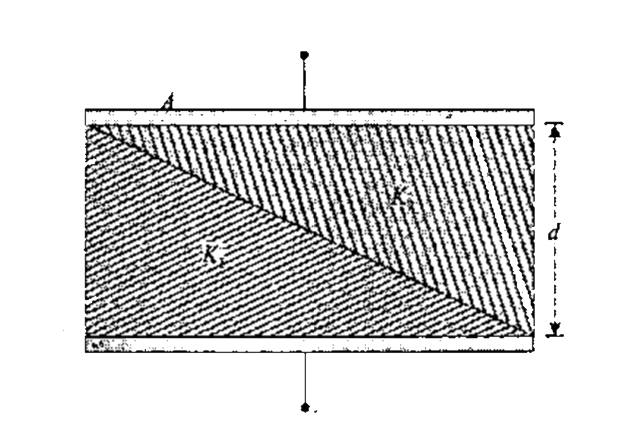
View Solution
Knowledge Check
A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.
 A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)
A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)A parallel plate capacitor having plate area 0.5m2 and plate separation of 5 mm is complete filled with a dielectric of dielectric constant 10. What is the instantaneous displacement current, if it is being charged at the rate of 100V/s? [ε0=8.85×10−12C2N/m2]
A8.85μAB0.885μAC0.177μAD1.77μAA parallel plate capacitor has capacitance of 1.0F. If the plates are 1.0mm apart, what is the area of the plates?
A1.1×105m2B2.1×108m2C0.5×108m2D1.6×108m2
The capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionA parallel plate capacitor has capacitance of 1.0F. If the plates are 1.0mm apart, what is the area of the plates?
View SolutionA parallel-plate capacitor having plate are 100cm2 and separation 1.0 mm holds a charge of 0.12μC when connected to a 120 V battery. Find the dielectric constant of the material filling the gap.
View SolutionA parallel plate air capacitor has plates of area 0.5 m2 and plate separation of 2 cm. if ε0=8.8×10−12C2/N−m2 then the capacitance of the capacitor is
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View Solution
