The position, velocity and acceleration of a particle moving with a constant acceleration can be represented by :
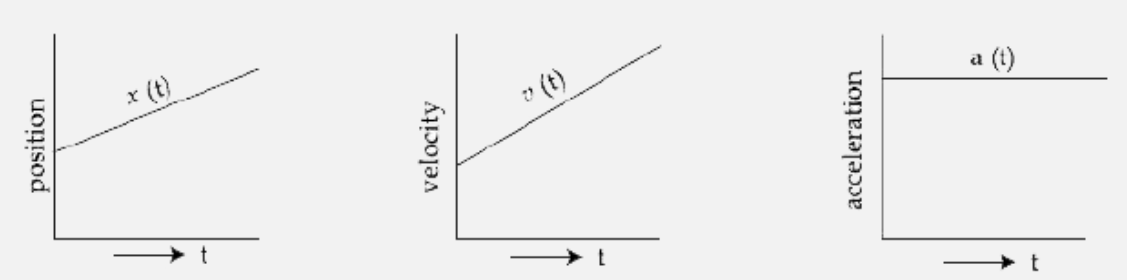

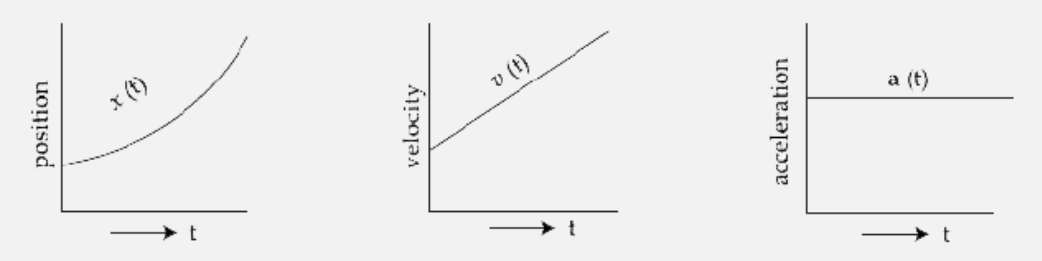
To solve the problem of determining how the position, velocity, and acceleration of a particle moving with constant acceleration can be represented, we will analyze the relationships between these quantities mathematically.
1. Understanding Constant Acceleration:
- When a particle moves with constant acceleration, its acceleration a does not change over time. This means that a is a constant value.
2. Velocity-Time Relationship:
- The relationship between velocity v and acceleration a is given by the equation:
v=u+at
where u is the initial velocity and t is the time. Since a is constant, this equation represents a linear relationship between velocity and time. Therefore, the velocity-time graph will be a straight line.
3. Position-Time Relationship:
- The position x of the particle can be expressed in terms of time t as:
x=ut+12at2
This equation shows that position is a quadratic function of time when acceleration is constant. Hence, the position-time graph will be a parabola.
4. Acceleration-Time Relationship:
- Since acceleration a is constant, the acceleration-time graph will be a horizontal line at the value of a.
5. Combining the Results:
- From the analysis:
- The acceleration-time graph is a horizontal line (constant).
- The velocity-time graph is a straight line (linear).
- The position-time graph is a parabola (quadratic).
- Therefore, the correct representation of the position, velocity, and acceleration of a particle moving with constant acceleration corresponds to the second option provided in the question.
Conclusion:
The correct answer is that the position, velocity, and acceleration of a particle moving with constant acceleration can be represented by the second option, which includes:
- A constant acceleration-time graph (horizontal line).
- A linear velocity-time graph (straight line).
- A parabolic position-time graph.
- When a particle moves with constant acceleration, its acceleration a does not change over time. This means that a is a constant value.
- The relationship between velocity v and acceleration a is given by the equation:
v=u+at
where u is the initial velocity and t is the time. Since a is constant, this equation represents a linear relationship between velocity and time. Therefore, the velocity-time graph will be a straight line.
- The position x of the particle can be expressed in terms of time t as:
x=ut+12at2
This equation shows that position is a quadratic function of time when acceleration is constant. Hence, the position-time graph will be a parabola.
- Since acceleration a is constant, the acceleration-time graph will be a horizontal line at the value of a.
- From the analysis:
- The acceleration-time graph is a horizontal line (constant).
- The velocity-time graph is a straight line (linear).
- The position-time graph is a parabola (quadratic).
- Therefore, the correct representation of the position, velocity, and acceleration of a particle moving with constant acceleration corresponds to the second option provided in the question.
The correct answer is that the position, velocity, and acceleration of a particle moving with constant acceleration can be represented by the second option, which includes:
- A constant acceleration-time graph (horizontal line).
- A linear velocity-time graph (straight line).
- A parabolic position-time graph.
Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:PHYSICS SECTION B
Explore 30 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:PHYSICS (SECTION B)
Explore 30 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
Knowledge Check
A particle is moving horizontally with constant acceleration.
AThe sum of the horizontal components of the forces acting on the particle is not zero.BThe sum of the vertical component of the forces acting on the particle is not zero.CThe forces acting on the particle are not in equilibrium.DAll of the above.Initial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle :
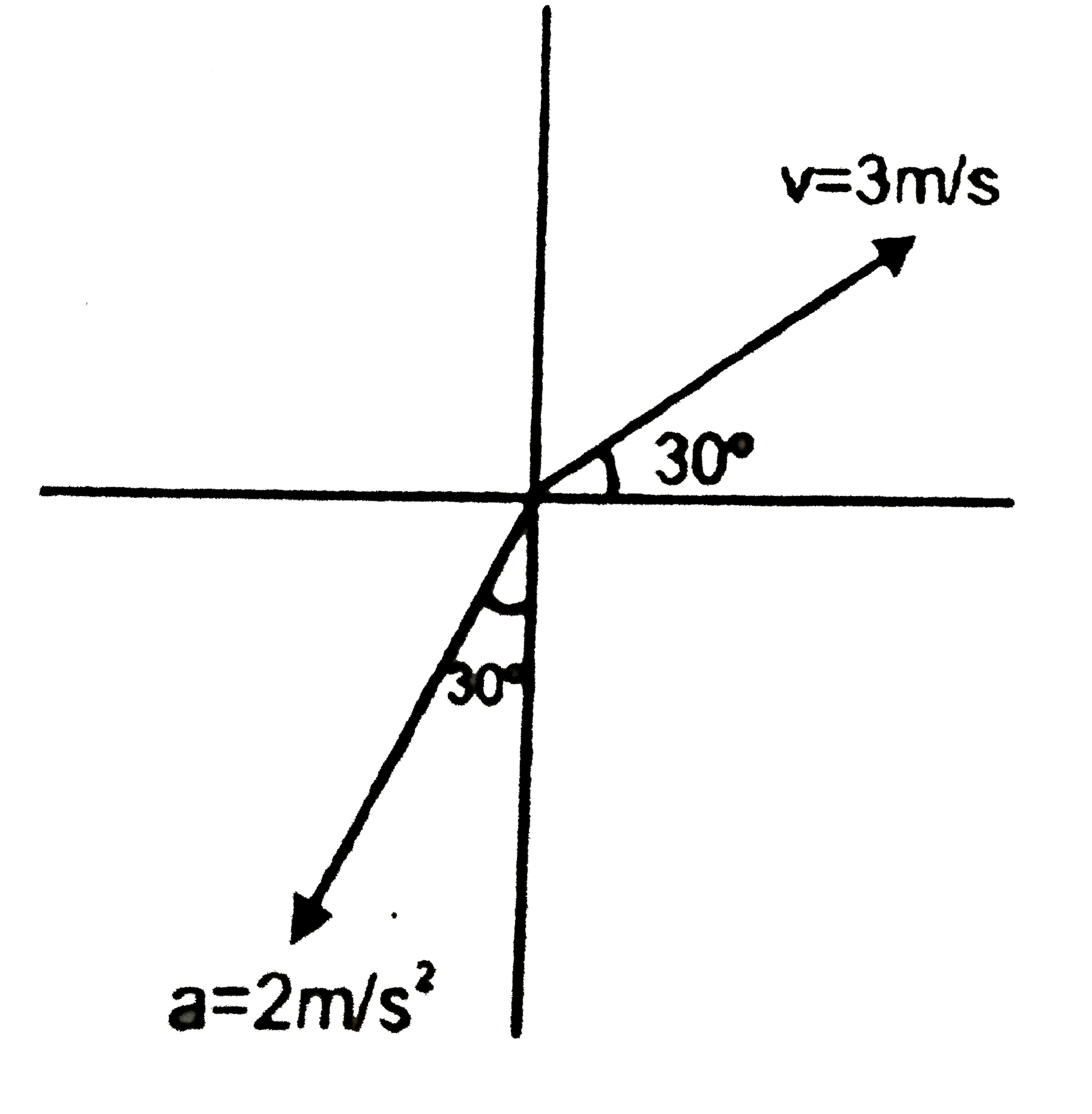 Ais 9m initiallyBis 9√3m initiallyCwill have minimum value of 98mDwill have minimum value 38m
Ais 9m initiallyBis 9√3m initiallyCwill have minimum value of 98mDwill have minimum value 38mWhich graph corresponds to an object moving with a constant negative acceleration and a positive velocity ?
A B
B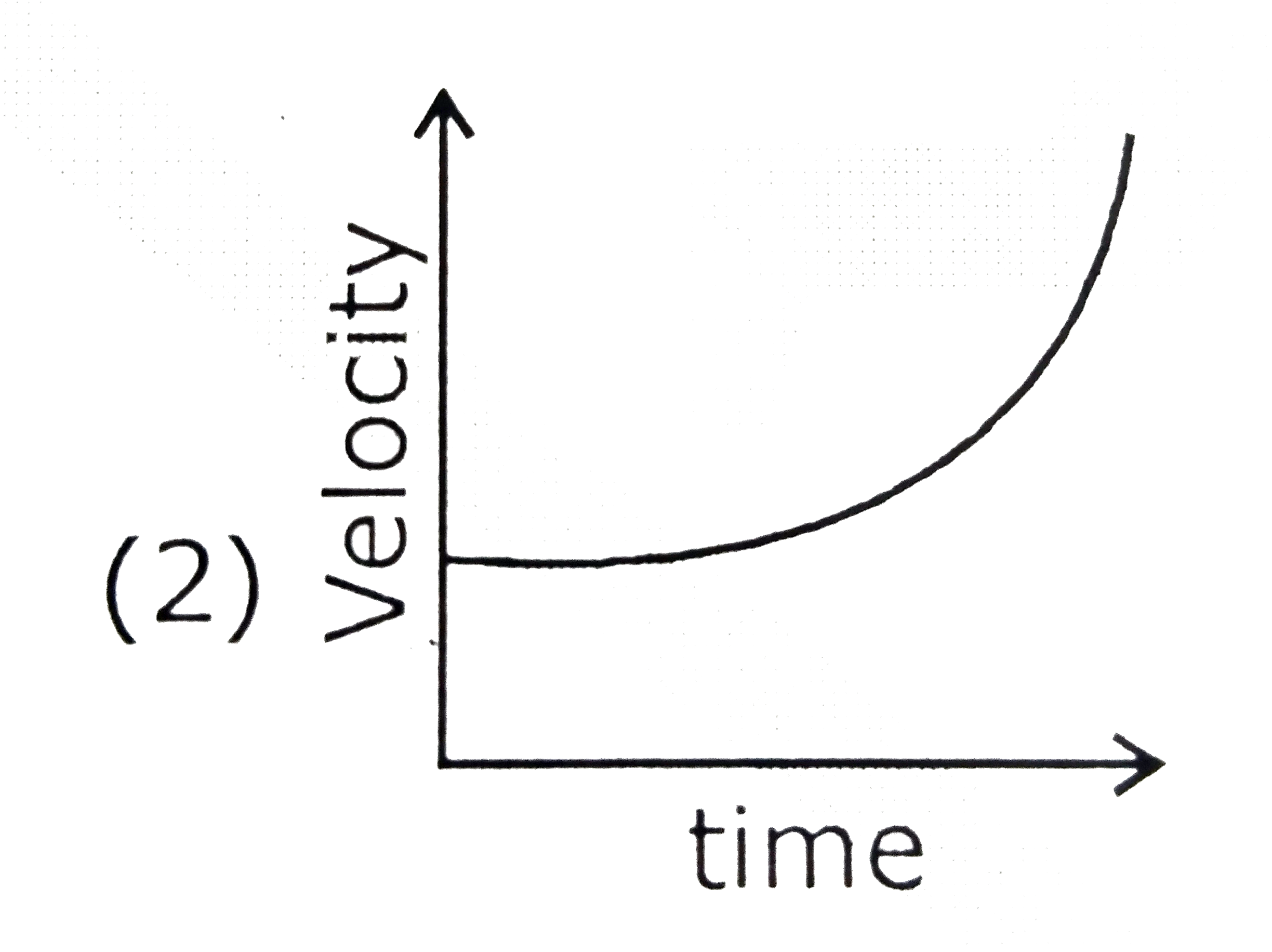 C
C D
D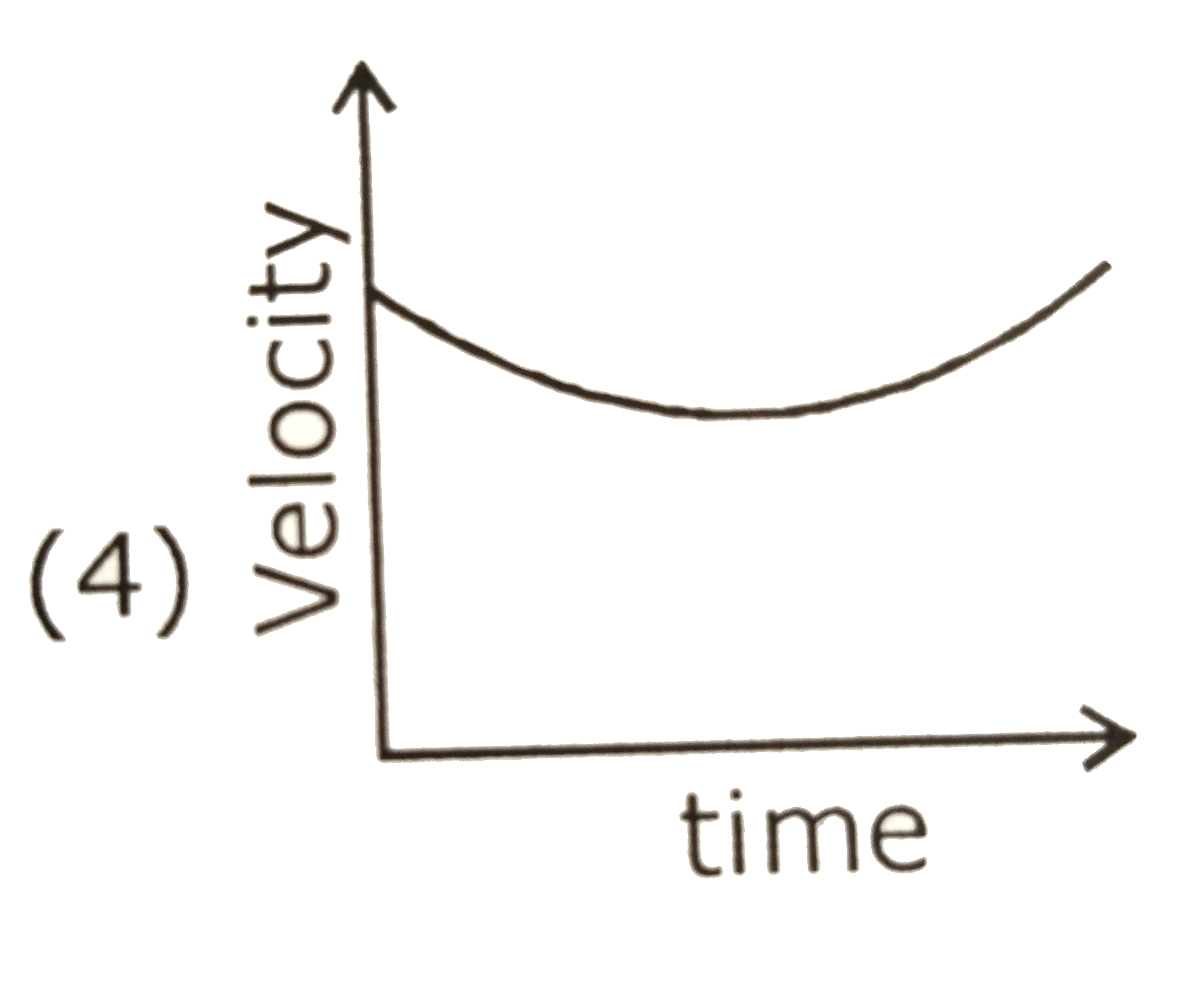
If a particle is moving with a constant velocity, what is its acceleration?
View SolutionThe acceleration vector of a particle moving with a uniform velocity is a ____ vector.
View SolutionGraphs are very useful to represent a physical situation. Various quantities can be easily represented on graphs and other quantites can be determined from the graph. For example the slope of velocity-time graph represents instantaneous acceleration. For a motion with constant acceleration slope of velocity-time graph is constant. If acceleration is changing with time, slope with change and thus velocity-time graph will be a non-linear curve. Further the area of velocity-time graph gives displacement.
The velocity-time graph for two objects P and Q are shown. The ratio of their respective acceleration is
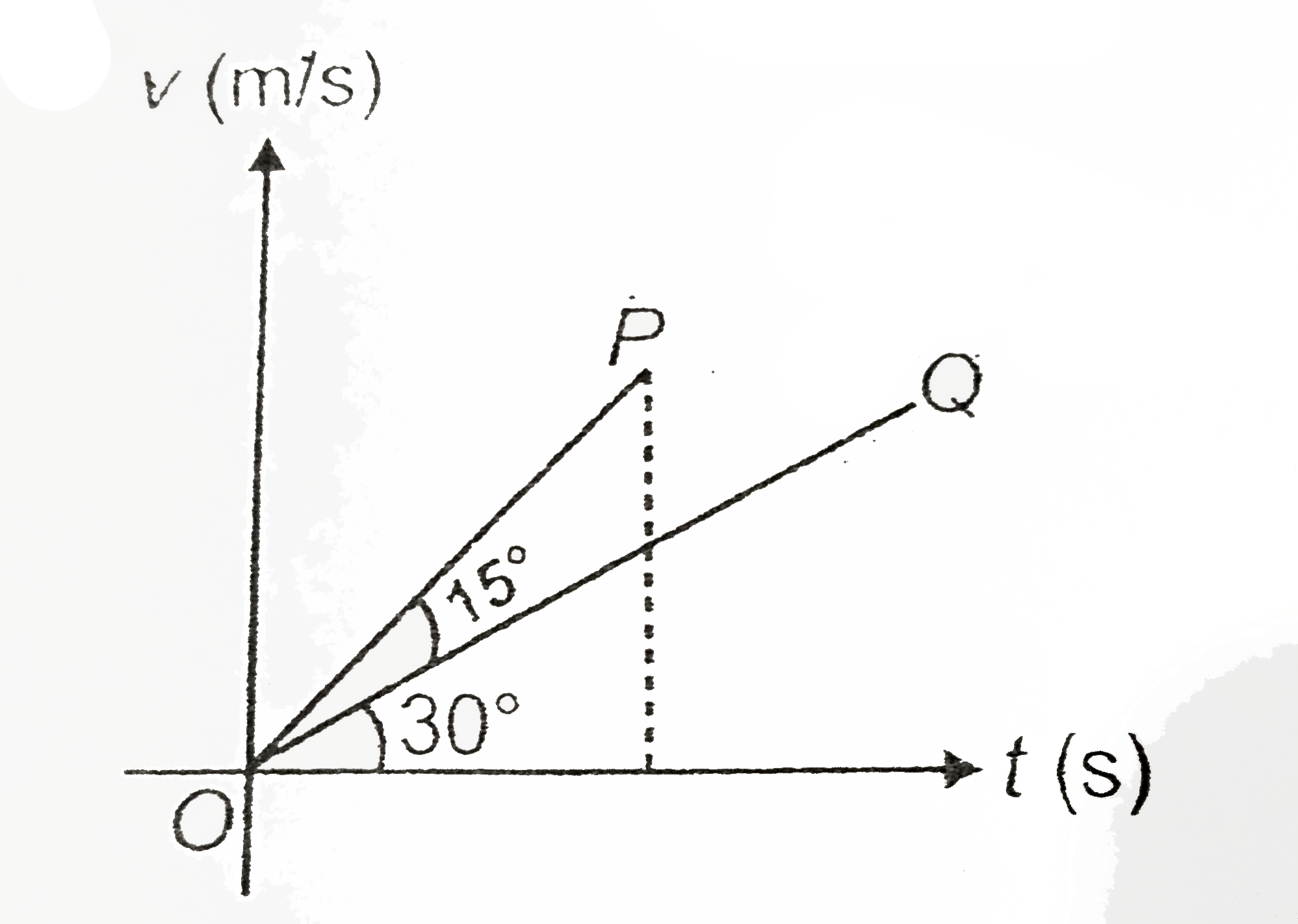
View SolutionGraphs are very useful to represent a physical situation. Various quantities can be easily represented on graphs and other quantites can be determined from the graph. For example the slope of velocity-time graph represents instantaneous acceleration. For a motion with constant acceleration slope of velocity-time graph is constant. If acceleration is changing with time, slope with change and thus velocity-time graph will be a non-linear curve. Further the area of velocity-time graph gives displacement.
For the given velocity-time graph the possibly correct acceleration-time relationship is

View SolutionA particle is moving in a circle with a constant speed, the acceleration of the particle has
View Solution