A parallel-plate capacitor has plates of unequal area . The larger plates is connected to the positive terminal of the battery and the smaller plate to its nagative terminal. Let Q+ and Q-be the charges appearing on the positive and negative plates respectively
Q+>Q−
Q=Q−
Q+<Q−
The information is not sufficient to decide the ralation between Q+ and Q.
The correct Answer is:B
To solve the problem regarding the charges on the plates of a parallel-plate capacitor with unequal areas, we will follow these steps:
Step 1: Understand the Configuration
We have a parallel-plate capacitor with two plates of unequal area. The larger plate is connected to the positive terminal of a battery, while the smaller plate is connected to the negative terminal.
Hint: Visualize the capacitor setup and identify which plate is connected to which terminal of the battery.
Step 2: Identify the Charges
When a capacitor is connected to a battery, the plate connected to the positive terminal accumulates a positive charge (Q+) and the plate connected to the negative terminal accumulates a negative charge (Q-).
Hint: Remember that the convention is that the positive charge appears on the plate connected to the positive terminal.
Step 3: Relate Charge to Voltage
The relationship between the charge (Q) on the plates of a capacitor and the voltage (V) across the capacitor is given by the equation:
Q=C⋅V
where C is the capacitance of the capacitor.
Hint: Capacitance (C) is a property of the capacitor and does not depend on the area of the plates in this context.
Step 4: Analyze the Capacitance
For a parallel-plate capacitor, the capacitance is given by:
C=ε0⋅Ad
where ε0 is the permittivity of free space, A is the area of the plates, and d is the distance between the plates. However, this does not affect the relationship between the charges on the plates.
Hint: Focus on the fact that the capacitance relates to the geometry of the plates but does not change the fundamental charge relationship.
Step 5: Conclude the Relationship Between Charges
Since the charges on the plates of a capacitor are equal in magnitude but opposite in sign, we can state:
|Q+|=|Q−|
This means that the positive charge on the larger plate (Q+) is equal in magnitude to the negative charge on the smaller plate (Q-).
Hint: Remember that in a capacitor, the total charge is conserved, leading to the conclusion that the magnitudes of the charges are equal.
Final Answer
Thus, we conclude that:
Q+=Q−
The correct option is:
Option 2: Q+ is equal to Q-.
We have a parallel-plate capacitor with two plates of unequal area. The larger plate is connected to the positive terminal of a battery, while the smaller plate is connected to the negative terminal.
When a capacitor is connected to a battery, the plate connected to the positive terminal accumulates a positive charge (Q+) and the plate connected to the negative terminal accumulates a negative charge (Q-).
The relationship between the charge (Q) on the plates of a capacitor and the voltage (V) across the capacitor is given by the equation:
Q=C⋅V
where C is the capacitance of the capacitor.
For a parallel-plate capacitor, the capacitance is given by:
C=ε0⋅Ad
where ε0 is the permittivity of free space, A is the area of the plates, and d is the distance between the plates. However, this does not affect the relationship between the charges on the plates.
Since the charges on the plates of a capacitor are equal in magnitude but opposite in sign, we can state:
|Q+|=|Q−|
This means that the positive charge on the larger plate (Q+) is equal in magnitude to the negative charge on the smaller plate (Q-).
Thus, we conclude that:
Q+=Q−
Option 2: Q+ is equal to Q-.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 2
6 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
65 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - worked out examples
23 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
A parallel plate capacitor is charged. If the plates are pulled apart
View SolutionEach plate of a parallel plate capacitor has a charge q on it. The capacitor is now connected to a battery. Now,
View SolutionIn a parallel plate capacitor with plate area A and charge Q, the force on one plate because of the charge on the other is equal to
View SolutionA parallel plate capacitor has capacitance of 1.0F. If the plates are 1.0mm apart, what is the area of the plates?
View SolutionA parallel plate capacitor is charged and then the battery is disconnected. When the plates of the capacitor are brought closer, then
View SolutionImagine a light planet revolving around a very massive star in a circular orbit of radius r with direction T. On what power of r, will the square of time period depends if the gravitational force of attraction between the planet and the star is proportional to r−5/2 .
View SolutionA parallel plate capacitor is charged and then isolated. On increasing the plate separation
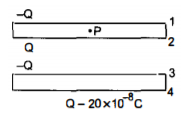
View SolutionThe nagative plate of a parallel plate capacitor is given a charge of −20X10−8C. Find the charges appearing on the four surface of the capacitor plates.
View SolutionA parallel plate capacitor is charged and the charging battery is then disconnected. If the plates of the capacitor are moved farther apart by means of insulating handles:
View SolutionA capacitor is composed of three parallel conducting plates. All three plates are of the same area A. The first pair of plates are kept a distance d1 apart, and the space between them is filled with a medium of a dielectric K1 . The corresponding data of the second pair are d2 and K2, respectively. The middle plate is connected to the positive terminal of a constant voltage source V and the external plates are connected the other terminal of V.

(a) Find the capacitance of the system .
(b) What is the surface charge density on the middle plate ?
(c) Compute the energy density in the medium K1
View Solution
