A partical moves from rest at A on the surface of a smooth circule cylinder of radius r as shown . At B it leavels the cylinder. The equation releaseder . The equation relating αandβ is

3sinα=2cosβ
2sinα=3cosβ
3sinβ=2cosα
2sinβ=3cosα
Step by step video & image solution for A partical moves from rest at A on the surface of a smooth circule cylinder of radius r as shown . At B it leavels the cylinder. The equation releaseder . The equation relating alpha and beta is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A particle moves from rest at A on the surface of a smooth circular cylinder of radius r as shown. At B it leaves the cylinder. Find the value of 4cosα3sinβ
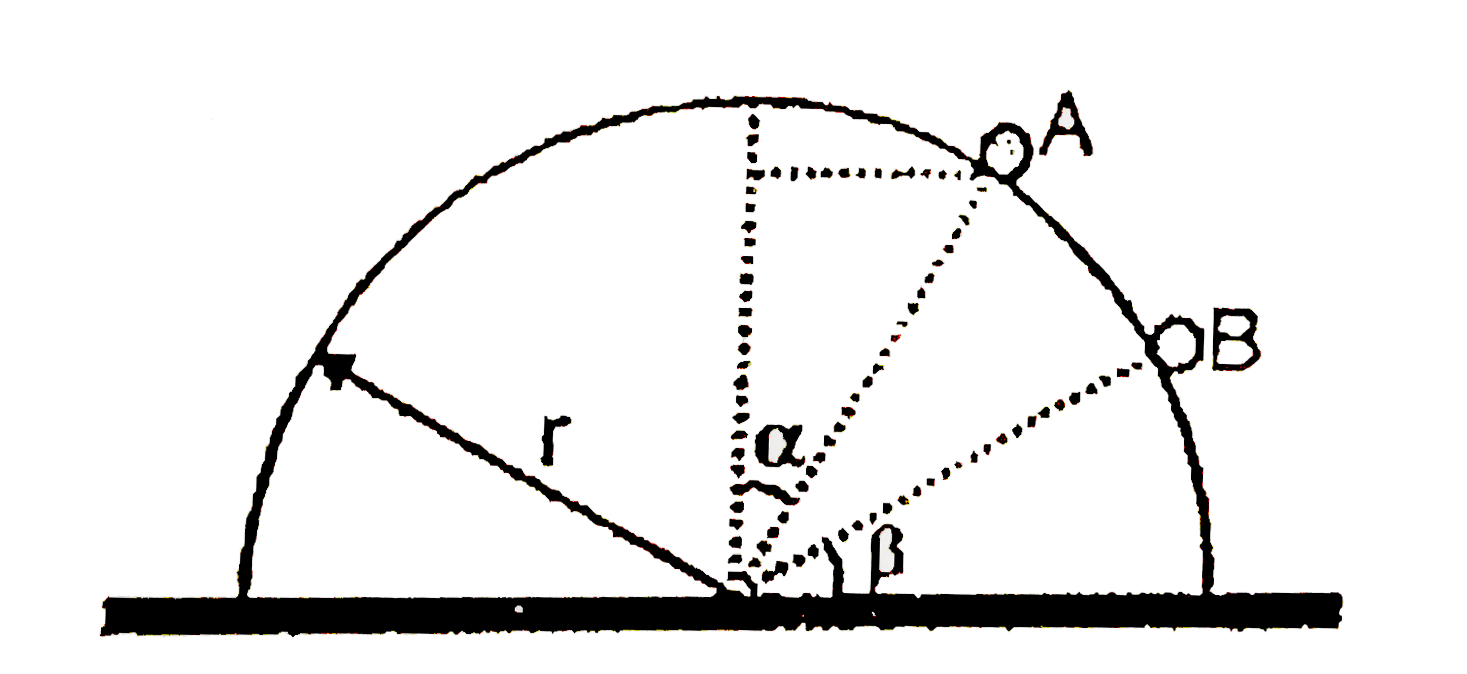
View SolutionA particle of mass m moves along the internal smooth surface of a vertical cylinder of radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0 and forms an angle α with the horizontal.
View Solution
Knowledge Check
A particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .A3sinθ=2cosθ'B2sinθ=3cosθ'C3sinθ'=2cosθD2sinθ=3cosθ'
.A3sinθ=2cosθ'B2sinθ=3cosθ'C3sinθ'=2cosθD2sinθ=3cosθ'A particle of mass m moves along the internal smooth surface of a vertical cylinder of the radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0. And forms an angle α with the horizontal.
AmV20Rsin2αBmV202Rcos2αC2mV20Rcos2αDmV20Rcos2αAn infinite cylinder of radius ro, carrying linear charge density λ. The equation of the equipotential surface for the cylinder is
Ar=r0eπε0[V(r)+V(r0)]λBr=r0e2πε0[V(r)−V(r0)]λ2Cr=r0e−2πε0[V(r)=V(r0)]λDr=r0e−2πε0[V(r)−V(r0)]λ
A block of mass M, with a semicircular track of radius R rest on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the point of the semicircular track. The cylinder slips in the semicircular frictionless track. How far the block moved when the cylinder reaches the bottom of the track ?
View SolutionAs shown in the adjacent figure, a sphere is placed in a cylinder. It touches the top, bottom and the curved surface of the cylinder. If radius of the base of the cylinder is 'r',
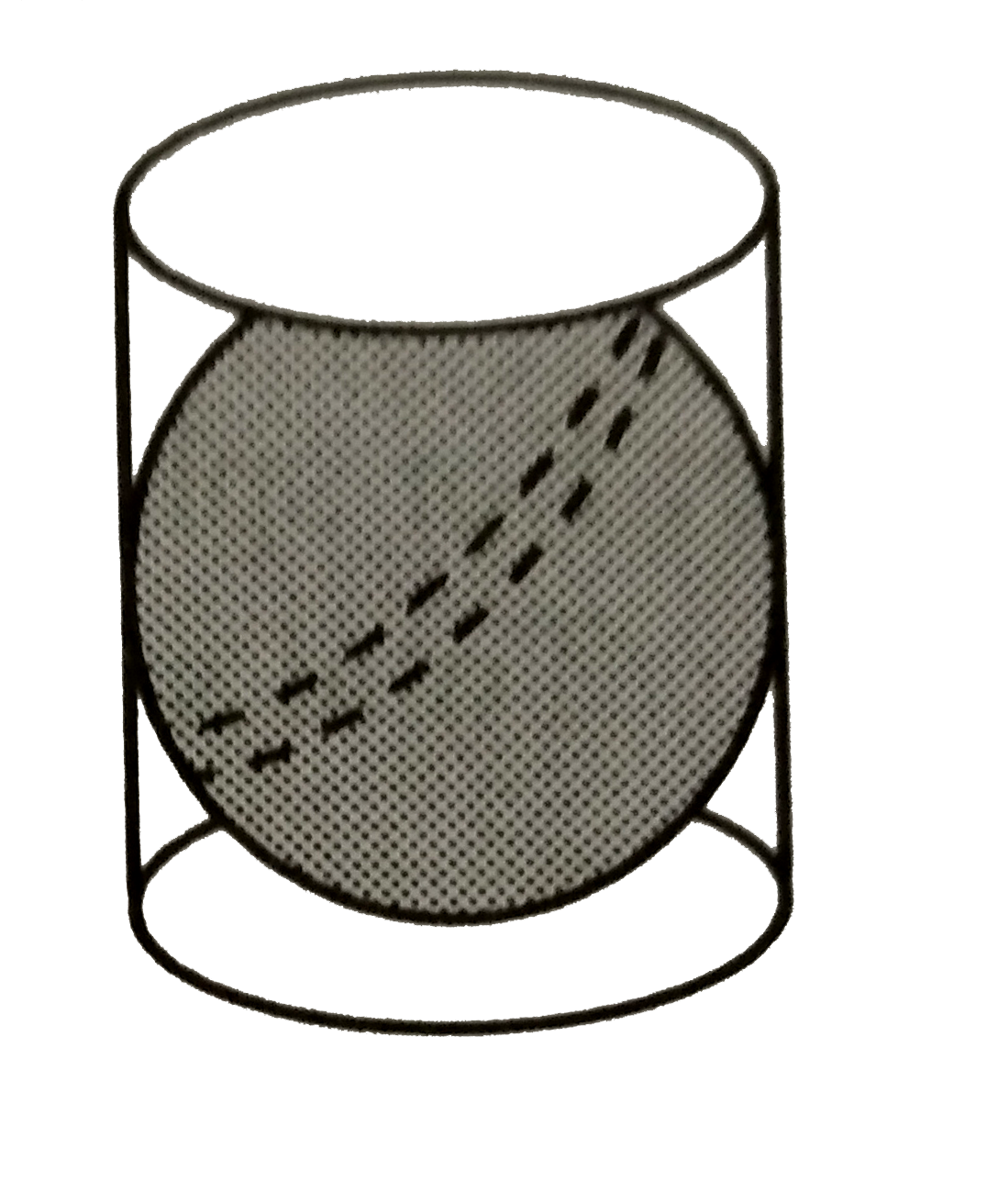
(i) what is ratio of the radii of the sphere and the cylinder?
(ii)what is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
(iii) what is the ratio of the volumes of the cylinder and the sphere?
View SolutionFrom a cylinder of radius R, a cylider of radius R/2 is removed, as shown in Fig. Current flowing in the remaining cylinder is I. Then, magnetic field strength is
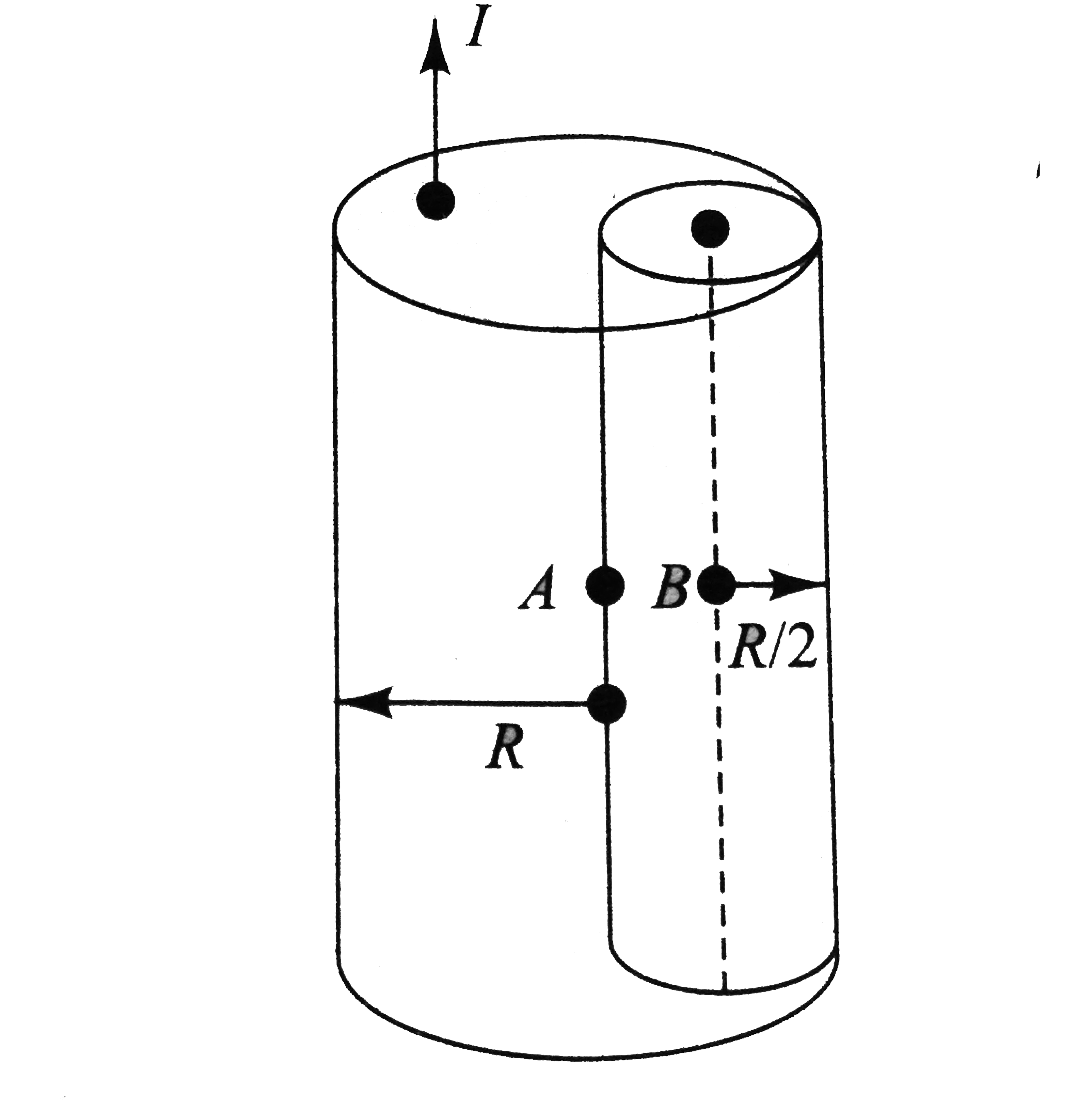
View SolutionFrom a cylinder of radius R, a cyclinder of radius R/2 is removed, as shown . Current flowing in the remaning cylinder is l. magnetic field strength is :

View Solution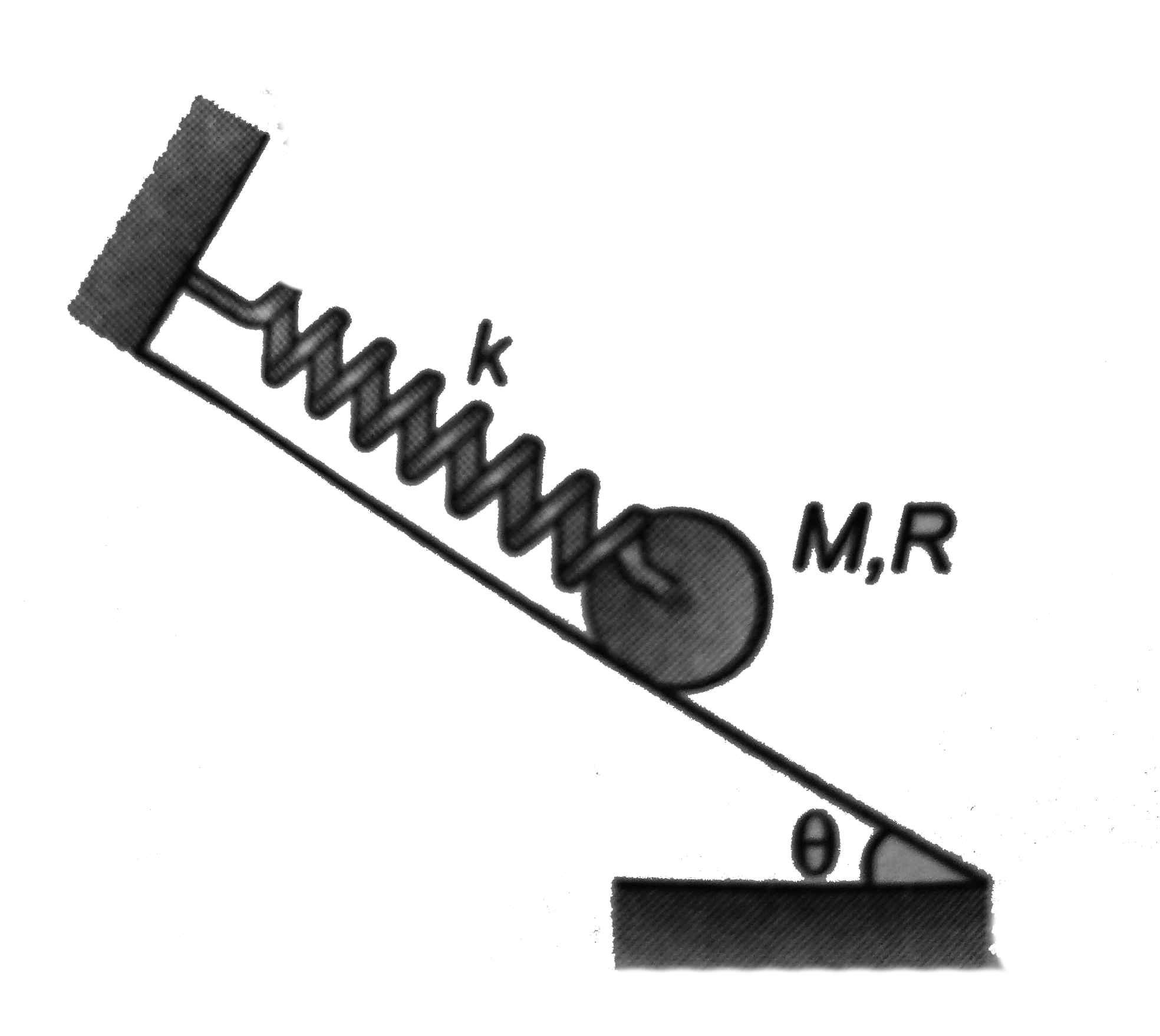
A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k is
View Solution
