An infinite cylinder of radius ro, carrying linear charge density λ. The equation of the equipotential surface for the cylinder is
r=r0eπε0[V(r)+V(r0)]λ
r=r0e2πε0[V(r)−V(r0)]λ2
r=r0e−2πε0[V(r)=V(r0)]λ
r=r0e−2πε0[V(r)−V(r0)]λ
The correct Answer is:C
Gaussian surface of radius r and length l.
According to Gauss's theorem
∮→E.→ds=qε0=λlε0
E(2πl)=λlε0orE=λ2πε0r ....(i)
∴V(r)−V(r0)=∫1r0→E→dl=λ2πε0loge.r0r
For an equipotenital surface of given V(r).
loge.rr0=2πε0λ[V(r)−V(r0)]
∴r=r0e−2πε0[V(r)−V(r0)]λ
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT Exemplar6videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT FINGERTIPSCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Assertion And Reason15videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT FINGERTIPSCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Van De Graaff Generator5videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT FINGERTIPSCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason15videos
ELECTROMAGNETIC WAVES
- BOOK - NCERT FINGERTIPSCHAPTER - MAGNETISM AND MATTER EXERCISE - Assertion And Reason15videos
MAGNETISM AND MATTER
Similar Questions
An infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View Solution
Knowledge Check
- Question 1 - Select One
An infinite sheet of charge has surface charge density σ . The separation between two equipotential surfaces, whose potential differ by V is:
AσV2∈0B2∈0VσC∈0VσD2σ∈0V - Question 2 - Select One
A coaxial cylinder made of glass is immersed in a-liquid of surface tension S. The radius of the inner and outer surface of the cylinder are R1andR2 respectively . Height till which liquid will rise is (Density of liquid is ρ )
A2SR2ρgB2SR1ρgCS(R2−R1)ρgD2S(R2−R1)ρg - Question 3 - Select One
A hollow cylinder having infinite length and carrying unifrom current per unit length λ along the circumference as shown Magnetic field inside the cylinder is
 .Aμ0λ2Bμ0λC2μ0λDnone
.Aμ0λ2Bμ0λC2μ0λDnone
There is infinitely long straight thread carrying a charge with linear density λ.Calculate the potential difference A and B.
 View Solution
View SolutionA charge q is placed at the centre of a cylinder of radius R and length 2R. Then electric flux through the curved surface of the cylinder is
View SolutionCalculate the moment of inertia of a hollow cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder?
View SolutionA sermicircular ring of radius R carries a uniform linear charge of λ. P is a point in the plane of the ring at a distance R from centre O. OP is perpendicular to AB. Find electric field intensity at point P.
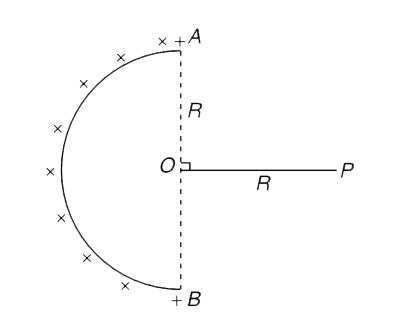 View Solution
View SolutionConsider an infinite line charge having uniform linear charge density and passing through the axis of a cylinder is removed.
 View Solution
View Solution

