A partical of mass $m$ moving with velocity $1 m / s$ collides perfectly elastically with another particle of mass $2 m$ . If the incident particle is deflected by $90^{\circ}$ . The heavy mass will make and angle $θ$ with the initial direction of $m$ equal to:

A

$60^{\circ}$

B

$45^{\circ}$

C

$15^{\circ}$

D

$30^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

From coservation of momentum along incident direction
$m \times 1 = 2 m v_{2} cos θ$ …….i
From conservation of momentum along perpendicular direction,
$m \times 0 + 2 m \times 0 = m v_{1} - 2 m v_{2} sin θ$
$\Rightarrow v_{1} = 2 v_{20 sin θ}$ …………ii

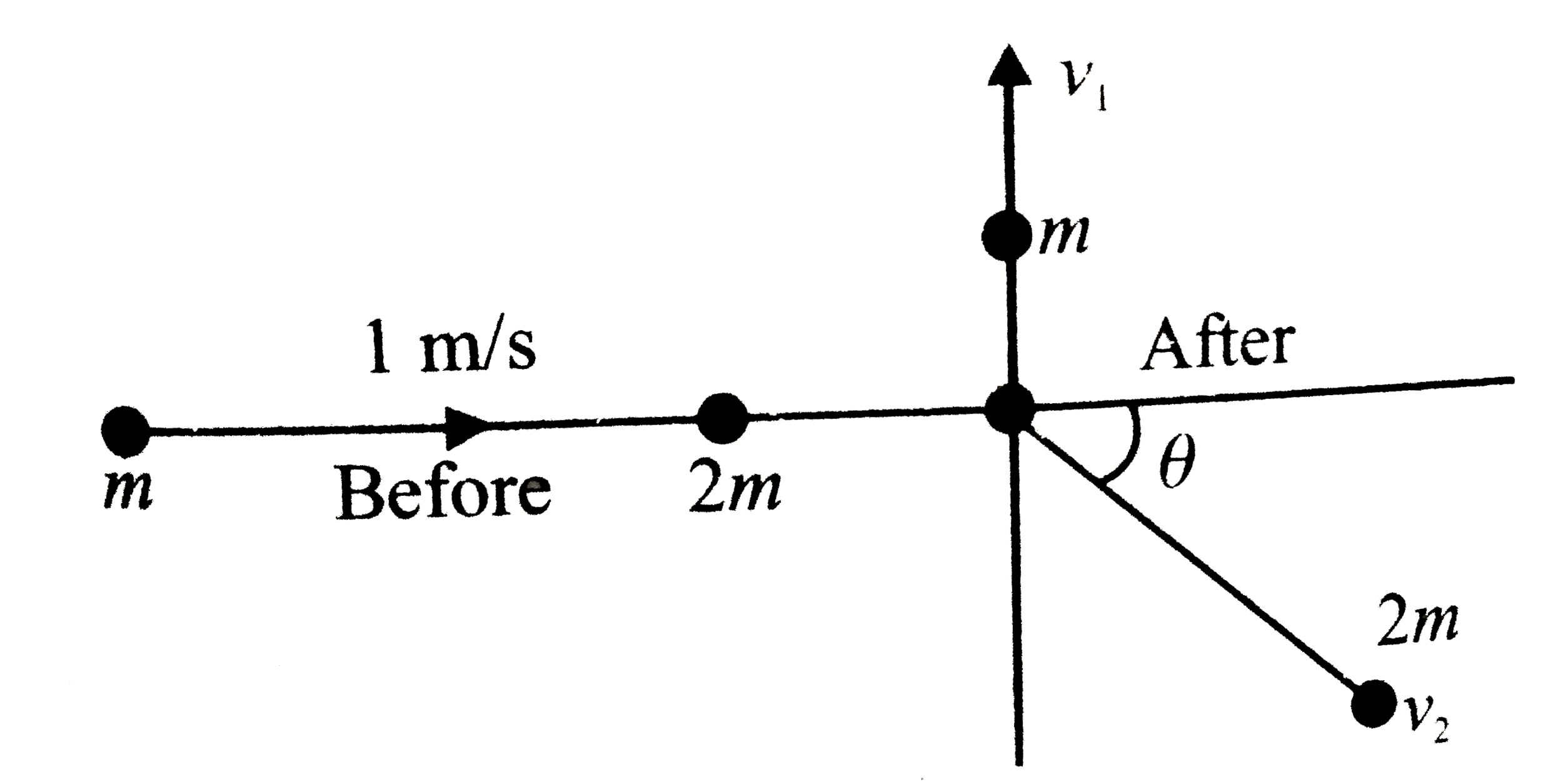
From energy conservartion
$\frac{1}{2} m \times {(1)}^{2} = \frac{1}{2} m v_{1}^{2} + \frac{1}{22} m v_{2}^{2}$ .......iii
From eqn i, ii and iii we get $θ = 306^{\circ}$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A partical of mass $m$ moving with velocity $1 m / s$ collides perfectly elastically with another particle of mass $2 m$ . If the incident particle is deflected by $90^{\circ}$ . The heavy mass will make and angle $θ$ with the initial direction of $m$ equal to:
A $60^{\circ}$
B $45^{\circ}$
C $15^{\circ}$
D $30^{\circ}$
Question 2 - Select One
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
A $\frac{3}{4} μ^{2}$
B $\frac{3}{8} μ^{2}$
C $\frac{1}{4} μ^{2}$
D $\frac{1}{8} μ^{2}$
Question 3 - Select One
A particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
A $\frac{v}{3}$
B $- \frac{v}{3}$
C $\frac{2 v}{3}$
D $\frac{- 2 v}{3}$

CENGAGE PHYSICS-CENTRE OF MASS-Single Correct

Home
Ask Doubt
Profile