A particle A of mass m moving on a smooth horizontal surface collides with a stationary particle B of mass 2m directly, situated at a distance d from a wall. The coefficient of restitution between A and B and between B and the wall is e = 1/4. Calculate the distance from the wall where they collide again. Assume that the entire motion takes place along a straight line perpendicular to the wall.
The correct Answer is:[12d/13]
Step by step video, text & image solution for A particle A of mass m moving on a smooth horizontal surface collides with a stationary particle B of mass 2m directly, situated at a distance d from a wall. The coefficient of restitution between A and B and between B and the wall is e = 1/4. Calculate the distance from the wall where they collide again. Assume that the entire motion takes place along a straight line perpendicular to the wall. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Advance McQ
20 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
Similar Questions
Block of mass m1 moving on a smooth horizontal surface,collides with a stationary block of mass m2 .The coefficient of restitution for the collision is e.The ratio m1m2 for which m1 is at rest after collision is
View SolutionA sphere A of mass m, travelling with speed v, collides directly with a stationary sphere B. If A is brought to rest and B is given a speed V, find (a) the mass of B (b) the coefficient of restitution between A and B?
View Solution
Knowledge Check
A particle (A) of mass m1 elastically collides with another stationary particle (B) of mass m2. Then :
Am1m2=12 and the particles fly a part in the opposite direction with equal velocities.Bm1m2=13 and the particles fly apart in the opposite direction with equal velocities.Cm1m2=21 and the collision angle between the particles is 60∘ symmetrically.Dm1m2=21 and the particles fly apart symmetrically at an angle 90∘A particle of mass m1 collides head on with a stationary particles of mass m2. If m1m2 gte, where e is the coefficient of restitution, then :
Am1 will retrun backBm1 will move in same directionCm1 will stopDunpredictableA partical of mass m1 collides head on with a stationary partical of mass m2. If m1m2>e where e is the coefficient of restitution, then :
Am1 will return backBm1 will move in same directionCm1 will stopDunpredicatable
Two particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Velocity of B after collision
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then
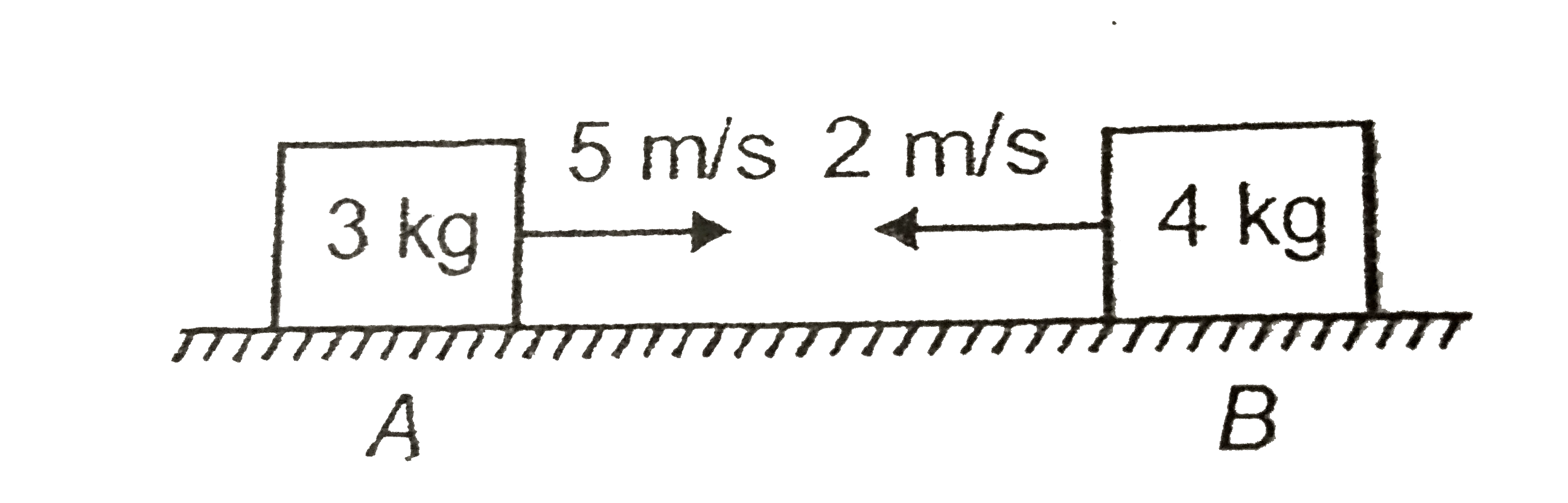
Velocity of A after collision
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Loss in kinetic energy in collision
View SolutionA particle moving on a smooth horizontal surface strikes a stationary wall. The angle of strike is equal to the angle of rebound & is equal to 37∘ and the coefficient of restitution with wall is e=15. Find the friction coefficient between wall and the particle form X10 and fill value of X :
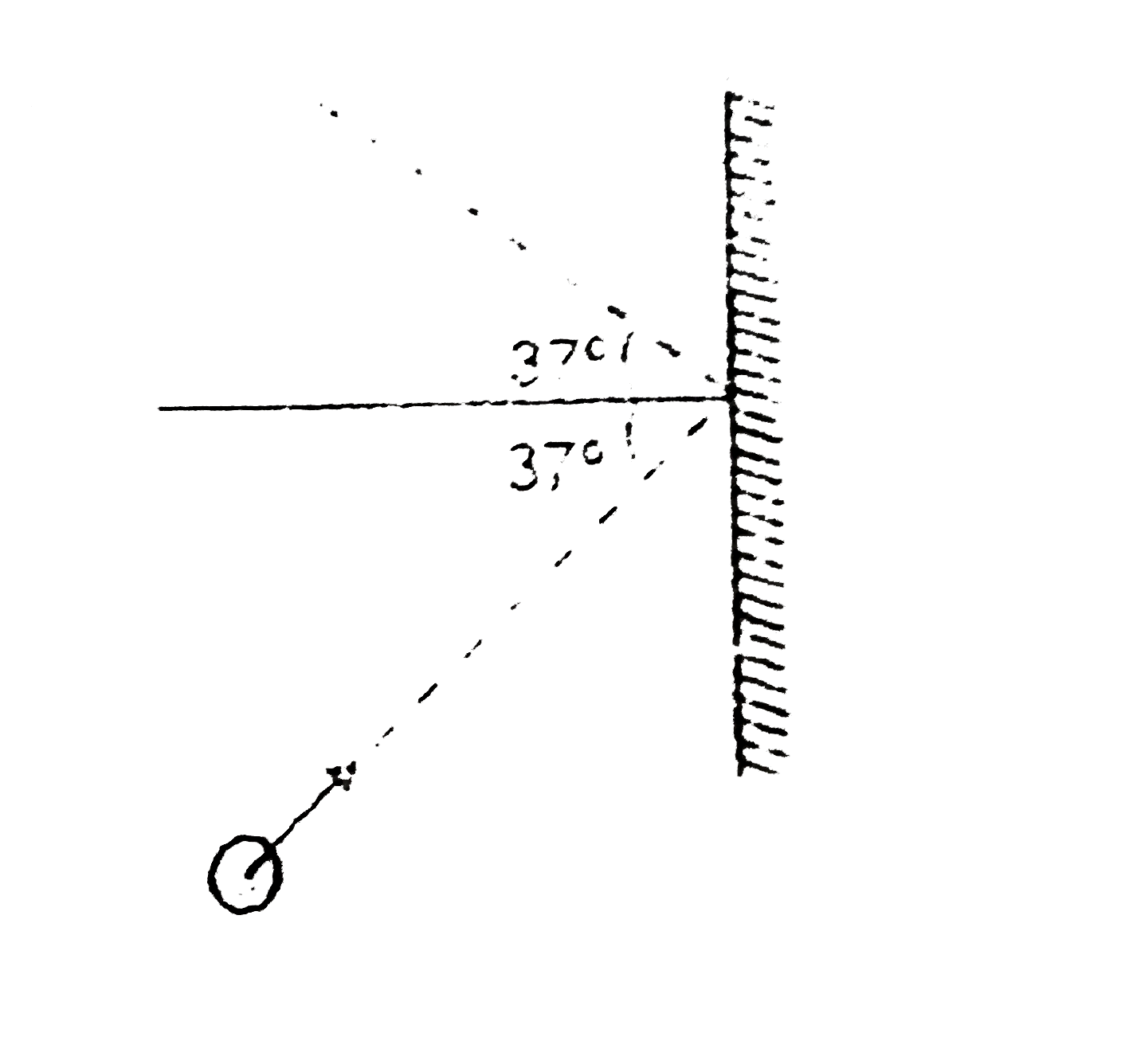
View SolutionA particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
View Solution
