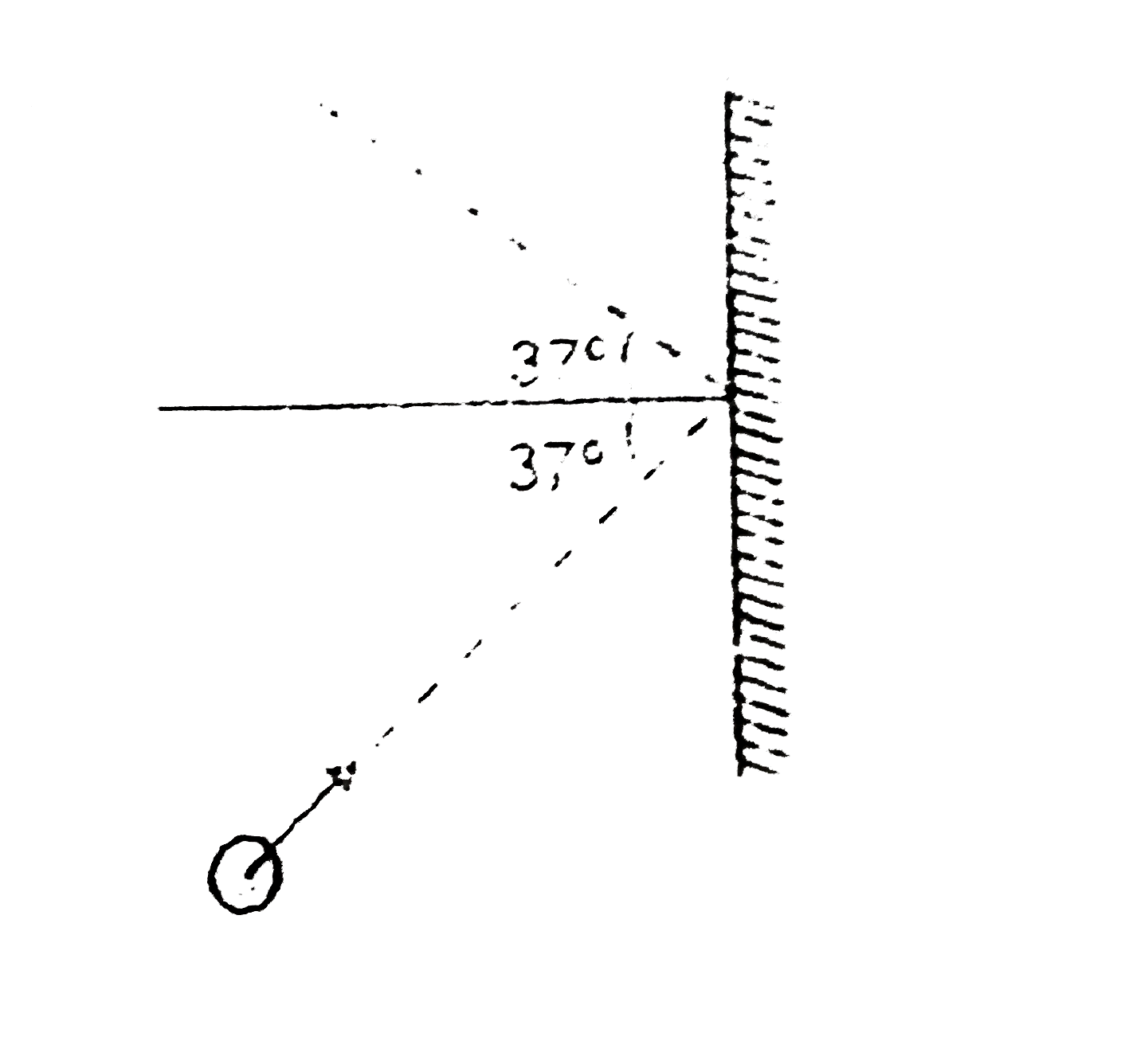
A particle moving on a smooth horizontal surface strikes a stationary wall. The angle of strike is equal to the angle of rebound & is equal to 37∘ and the coefficient of restitution with wall is e=15. Find the friction coefficient between wall and the particle form X10 and fill value of X :
The correct Answer is:5
Since e=15
∴ Final normal component of velocity
=vcos37∘5
As the angle of rebound is equal to the angle before impact.
Therefore, both normal & tangential components of velocities must change by the same factor.
∴ Tangential velocity after impact becomes vsin37∘5
Let the time of impact be Δt
N=m(vcos37∘+vcos37∘5)Δt=6mvcos3725Δt
wher N is the normal force imparted on the ball by the wall.
Frictional force =μN=65μmvcos37∘Δt
Also frictional force
=m[vsin372−vsin37∘5]Δt
⇒m[vsin37∘−vsin37∘5]Δt
=65μmvcos37∘Δt
⇒μ=23tan37∘
⇒μ=23.34=12.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.609videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.6120videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.5820videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A particle strikes a smooth horizontal surface at an angle θ>0 and it rebounds at an angle ϕ as shown
 View Solution
View SolutionA particle A of mass m moving on a smooth horizontal surface collides with a stationary particle B of mass 2m directly, situated at a distance d from a wall. The coefficient of restitution between A and B and between B and the wall is e = 1/4. Calculate the distance from the wall where they collide again. Assume that the entire motion takes place along a straight line perpendicular to the wall.
View Solution
Knowledge Check
- Question 1 - Select One
In the figure shown a particle P strikes the inclined smooth plane horizontally and rebounds vertically if the angle θ is 60∘ then the coefficient of restitution is:
 A1/3B1/√2C1/2D1
A1/3B1/√2C1/2D1 - Question 2 - Select One
A particle strikes a smooth horizontal surface at an angle of 45∘ with a velocity of 100m/s and rebounds. If the coefficient of restitution between the floor and the particle is 0.57 then the angle which the velocity of the particle after it rebounds will make with the floor is
A30∘B45∘C60∘D90∘ - Question 3 - Select One
A particle moving with a velocity of (4ˆi−ˆj ) mis strikes a fixed smooth wall and finally moves with a velocity of (3ˆi+2ˆj) m/s. The coefficient of restitution between the wall and the particle in the collision will be
A73B37C√1317D√1713
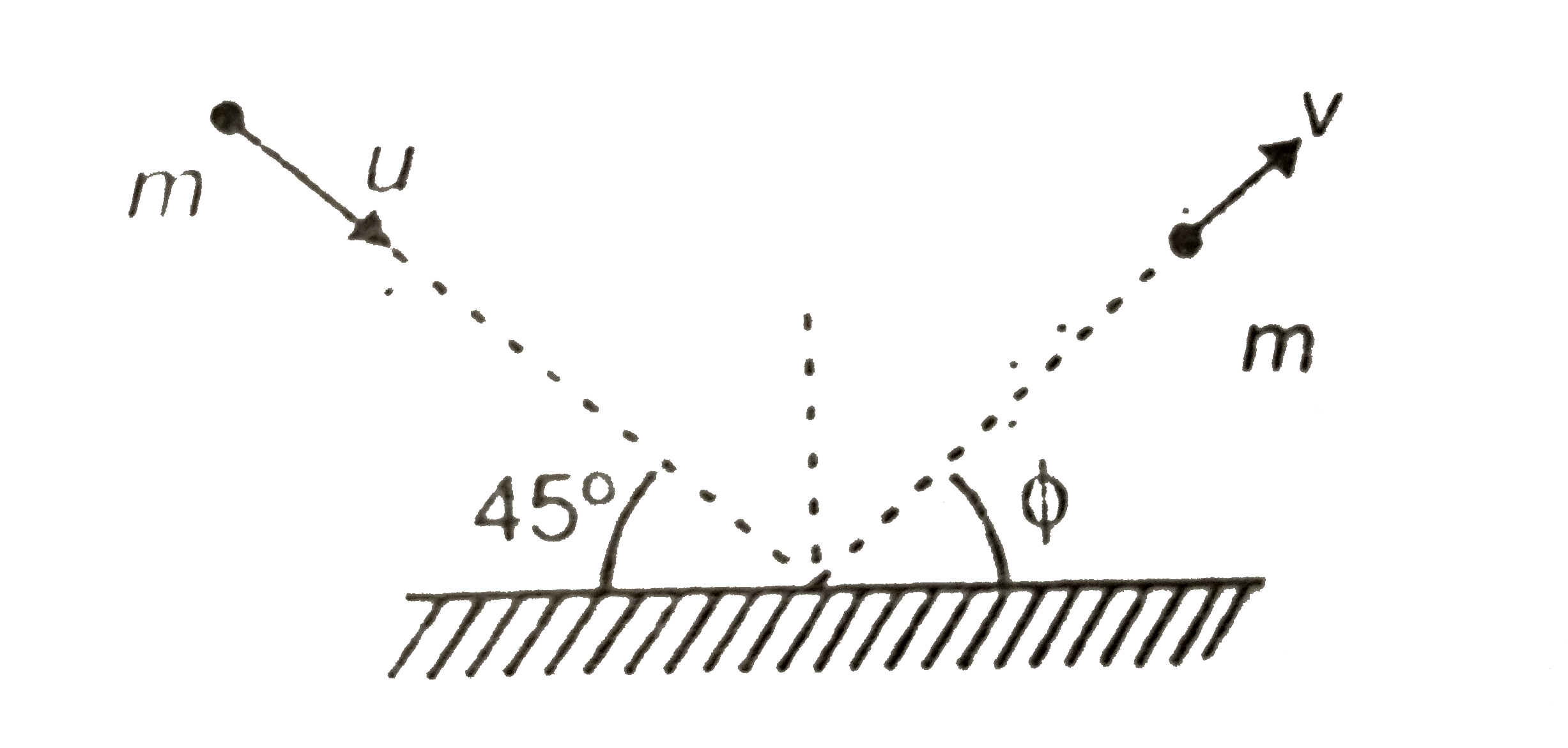
A particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is
 View Solution
View SolutionA particle of mass m strikes on ground with angle of incidence 45∘. If coefficient of restitution, e=1√2, find the velociy after impact and angle of reflection.
View SolutionA smooth sphere is moving on a horizontal surface with velocity vector 2ˆi+2ˆj immediately before it hits a vertical wall. The wall is parallel to ˆj and the coefficient of restitution of the sphere and the wall is e=12. Find the velocity of the sphere after it hits the wall?
View SolutionA ball is given velocity u=√3gd at an angle 45∘ with horizontal. It strikes a wall at distance d and returns to its original position. Find the coefficient of restitution e.
View SolutionA smooth sphere is moving on a horizontal surface with velocity vector 3ˆi+ˆj immediately before it hits a vertical wall. The wall is parallel to the vector ˆj and the coefficient of restitution between the wall and sphere is 13. The velocity vector of the sphere after it hits the wall is :-
View Solution

