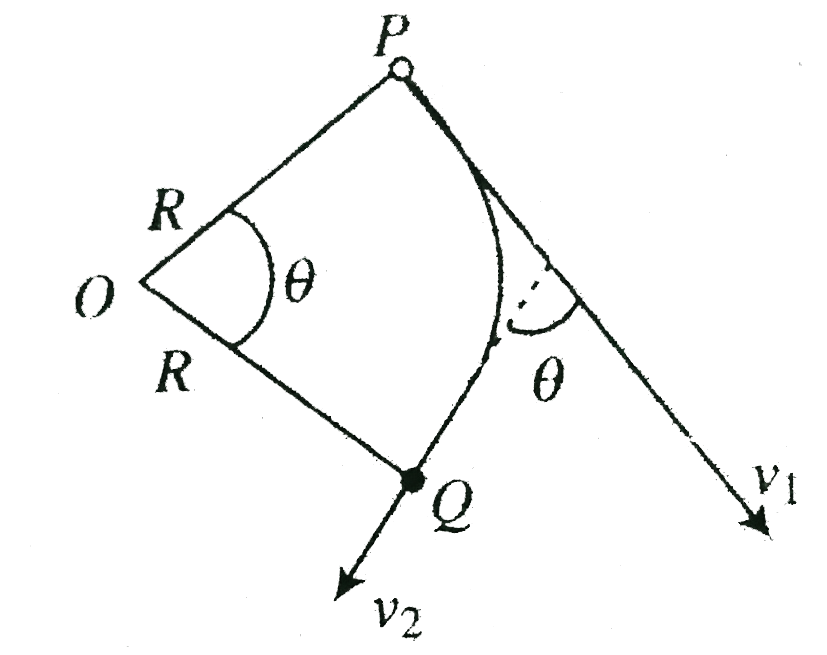
A particle describes an angle $θ$ in a circular path with a constant speed $v$ . Find the $a$ charge in the velocity of the particle and $b$ average acceleration of the particle during the motion in the curve (circle).
.

Video Solution

Text Solution

Verified by Experts

a. As the particle moves from $P$ to $Q$ . The velocty turns through an angle $θ$ . Then,
$| Δ \to v | = \sqrt{v_{1}^{2} + v_{2}^{2} - 2 v_{1} v_{2} cos θ}$
$= \sqrt{v^{2} + v^{2} - 2 \lor cos θ} = 2 v sin (\frac{θ}{2})$
b. The time of motion is $Δ t = R θ / v$ . Then, average acceleration is $| {\to a}_{a v} | = \to v Δ$ .
Substituting $| Δ \to v |$ and $Δ$ , we have $| {\to a}_{a V} | = \frac{2 v sin (\frac{θ}{2})}{\frac{R θ}{v}} = sin (\frac{θ}{2})$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
the circular motion of a particle with constant speed is
ASimple harmonic but not periodic
BPeriodic and simple harmonic
Cneither periodic nor simple harmonic
Dperiodic but not simple harmonic
Question 2 - Select One
During a accelerated motion of a particle
Aaverage velocity of the particle is always less than its final velocity
Baverage velociyt of the particle is always greater than its final velocity
Caverage velocity of the particle may be zero also
Daverage velocity of the particle is half its final velocity
Question 3 - Select One
If a particle is moving along a circular path with constant speed, then Its motion is
APeriodic and simple harmonic
BNon periodic
CPeriodic but not simple harmonic
DNon periodic but simple harmonic

CENGAGE PHYSICS-KINEMATICS-1-Integer

Home
Ask Doubt
Profile