A particle has co-ordinates (x, y). Its position vector makes on angle $θ$ with positive x direction. In an infinitesimally small interval of time the particle moves such that length of its position vector does not change but angle $θ$ increases by $d θ$ . Express the change in position vector of the particle in terms of x, y, $d θ$ and unit vectors $ˆ i$ and $ˆ j$ .

Video Solution

Answer

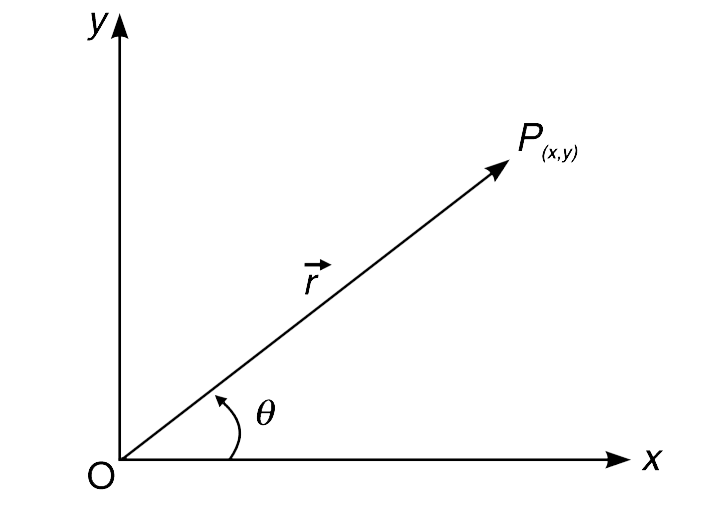
Step by step video & image solution for A particle has co-ordinates (x, y). Its position vector makes on angle theta with positive x direction. In an infinitesimally small interval of time the particle moves such that length of its position vector does not change but angle theta increases by d theta. Express the change in position vector of the particle in terms of x, y, d theta and unit vectors hati and hatj. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A vector of length $l$ is turned through the angle $θ$ about its tail. What is the change in the position vector of its head ?
A $l cos (θ / 2)$
B $2 l sin (θ / 2)$
C $2 l cos (θ / 2)$
D $l sin (θ / 2)$
Question 2 - Select One
A vector $\to A$ is rotated through angle $θ$ about its tail. Change of position vector of its tip of is:
A $A sin θ$
B $2 A cos . \frac{θ}{2}$
C $2 A sin . \frac{θ}{2}$
D $A cos θ$
Question 3 - Select One
A particle moves in a plane such that its coordinates changes with time as $x = a t$ and $y = b t$ , where a and b are constants. Find the position vector of the particle and its direction at any time t.
A $(a) ˆ i + (b t) ˆ j$
B $(a t) ˆ i + (b) ˆ j$
C $(a t) ˆ i + (b t) ˆ j$
D $(a) ˆ i + (b) ˆ j$

ANURAG MISHRA-DESCRIPTION OF MOTION-Example

Home
Ask Doubt
Profile

Topper's Solved these Questions

Similar Questions

Knowledge Check

A vector of length l is turned through the angle θ about its tail. What is the change in the position vector of its head ?

A vector →A is rotated through angle θ about its tail. Change of position vector of its tip of is:

A particle moves in a plane such that its coordinates changes with time as x=at and y=bt, where a and b are constants. Find the position vector of the particle and its direction at any time t.

ANURAG MISHRA-DESCRIPTION OF MOTION-Example

A vector of length $l$ is turned through the angle $θ$ about its tail. What is the change in the position vector of its head ?

A vector $\to A$ is rotated through angle $θ$ about its tail. Change of position vector of its tip of is:

A particle moves in a plane such that its coordinates changes with time as $x = a t$ and $y = b t$ , where a and b are constants. Find the position vector of the particle and its direction at any time t.