A particle is given velocity 3m/s along the positive x-axis subjected to constant accelaration 4m/s2 along the positive y-axis. Find the distaplacement of the particle in 2s and trajectory followed by the particle.
To solve the problem step by step, we will calculate the displacement of the particle after 2 seconds and determine the trajectory it follows.
Step 1: Identify the initial conditions
- Initial velocity along the x-axis, ux=3m/s
- Initial velocity along the y-axis, uy=0m/s (since there is no initial velocity in the y-direction)
- Acceleration along the y-axis, ay=4m/s2
- Time, t=2s
Step 2: Calculate the displacement in the x-direction
Displacement in the x-direction can be calculated using the formula:
sx=ux⋅t
Substituting the values:
sx=3m/s⋅2s=6m
Step 3: Calculate the displacement in the y-direction
Displacement in the y-direction can be calculated using the formula:
sy=uy⋅t+12ayt2
Since uy=0:
sy=0+12⋅4m/s2⋅(2s)2
Calculating this:
sy=12⋅4⋅4=8m
Step 4: Calculate the resultant displacement
The resultant displacement R can be found using the Pythagorean theorem:
R=√s2x+s2y
Substituting the values:
R=√(6m)2+(8m)2=√36+64=√100=10m
Step 5: Calculate the angle of displacement
The angle θ with respect to the positive x-axis can be calculated using:
tanθ=sysx
Substituting the values:
tanθ=86=43
Thus,
θ=tan−1(43)≈53∘
Step 6: Write the final displacement and angle
The displacement of the particle after 2 seconds is:
R=10mat an angle53∘with the positive x-axis.
Step 7: Determine the trajectory of the particle
The equations of motion for the x and y coordinates are:
- For x:
x(t)=ux⋅t=3t
- For y:
y(t)=12ayt2=2t2
To find the trajectory, we eliminate t from these equations. From the equation for x:
t=x3
Substituting this into the equation for y:
y=2(x3)2=2⋅x29=29x2
Final Result
The trajectory followed by the particle is:
y=29x2
This represents a parabolic path opening upwards.
- Initial velocity along the x-axis, ux=3m/s
- Initial velocity along the y-axis, uy=0m/s (since there is no initial velocity in the y-direction)
- Acceleration along the y-axis, ay=4m/s2
- Time, t=2s
Displacement in the x-direction can be calculated using the formula:
sx=ux⋅t
Substituting the values:
sx=3m/s⋅2s=6m
Displacement in the y-direction can be calculated using the formula:
sy=uy⋅t+12ayt2
Since uy=0:
sy=0+12⋅4m/s2⋅(2s)2
Calculating this:
sy=12⋅4⋅4=8m
The resultant displacement R can be found using the Pythagorean theorem:
R=√s2x+s2y
Substituting the values:
R=√(6m)2+(8m)2=√36+64=√100=10m
The angle θ with respect to the positive x-axis can be calculated using:
tanθ=sysx
Substituting the values:
tanθ=86=43
Thus,
θ=tan−1(43)≈53∘
The displacement of the particle after 2 seconds is:
R=10mat an angle53∘with the positive x-axis.
The equations of motion for the x and y coordinates are:
- For x:
x(t)=ux⋅t=3t
- For y:
y(t)=12ayt2=2t2
t=x3
Substituting this into the equation for y:
y=2(x3)2=2⋅x29=29x2
The trajectory followed by the particle is:
y=29x2
This represents a parabolic path opening upwards.
Topper's Solved these Questions
Similar Questions
A particle is given velocity 4m/s along the positive y-axis subjected to constant accelaration 10m/s2 at 53∘ with the x-axis. Find the distaplacement of a particle along the coordinate axes after 3s.
View SolutionAt t=0, the particle is at the origin and its velocity is 10m/s at an angle 37∘ with the x-axis. The particle moves in x−y plane with a constant acceleration of 1m/s2 along the y-axis. Find the magnitude and direction of the velocity after 2s.
View Solution
Knowledge Check
Three particles starts from origin at the same time with a velocity 2ms−1 along positive x-axis, the second with a velocity 6ms−1 along negative y-axis, Find the velocity of the third particle along x=y line so that the three particles may always lie in a straight line.
A−3√3B3√2C−3√2D2√2A particle moves along a straight line parallel to x-axis at a distancce d=3m from it, with constant speed of v=3m/s. Another particle stats from the origin with constant acceleration a=4m/s2 at an angle θ with y-axis along a straight line at the instant the first particle crosses y-axis. Find 'theta' such that the two particle collide.
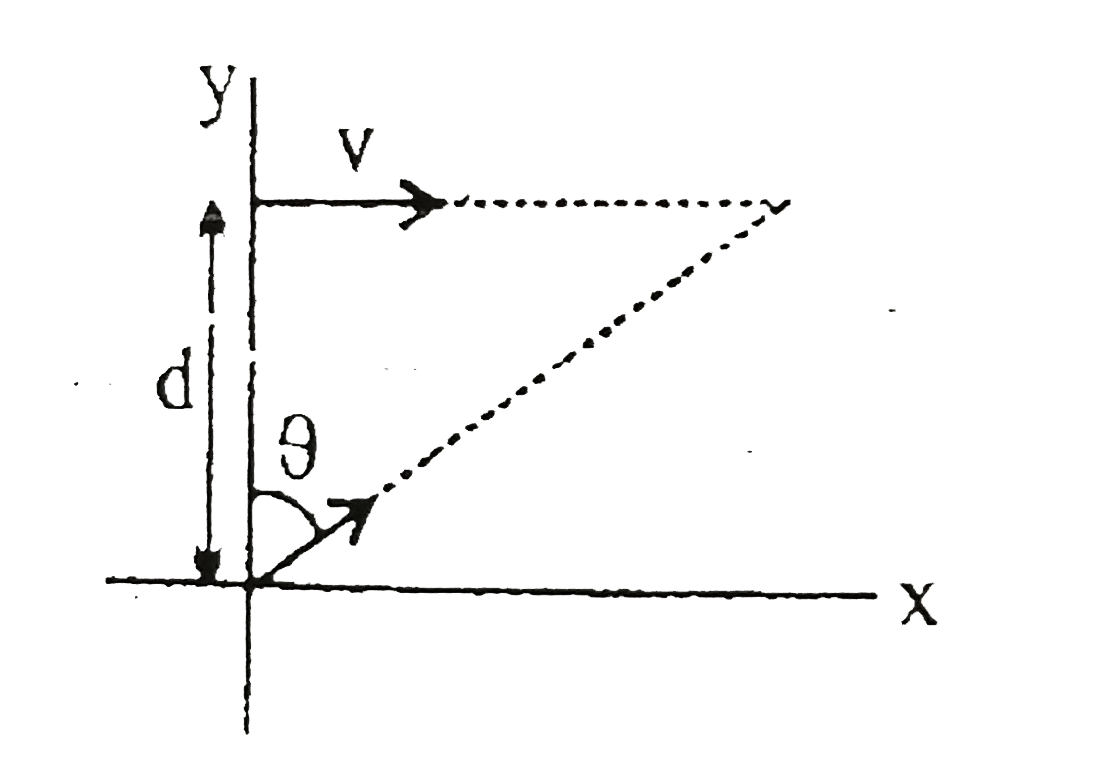 A0∘B30∘C45∘D60∘
A0∘B30∘C45∘D60∘A particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
AThe maximum displacement of the particle from the starting point is u√bBThe particle will oscillate about the originCVelocity is maximum at the originDGiven data is insufficient to determine the exact motion of the particle.
Two particles are moving along x-axis. Particle-1 starts from x=−10m with velocity 4m/s along negative x-direction and acceleration 2m/s2 along positive x-direction. Particle-2 starts from x=+2m with velocity 6m/s along positive x-direction and acceleration 2m/s2 along negative x-direction.
(a) Find the time when they collide.
(b) Find the x-coordinates where they collide. Both start simultaneously.
View SolutionA particle is moving along a straight line along x-zxis with an initial velocity of 2m/s towards positive x-axis. A constant acceleration of 0.5m/s2 towards negative x-axis starts acting on particle at t=0. Find velocity (in m/s) of particle at t=2s.
View SolutionA particle experience an acceleration a=(4e−3t),m/s2 along positive x-axis,where t is time in s.If the initial velocity of the particle is 2m/s along positive x -axis,the velocity of the particle when its acceleration becomes zero is ?
View SolutionA particle experience an acceleration a=(4e−3t)ms2 along positive x-axis, where t is time in s .If the initial velocity of the particle is 2m/s along positive x-axis,the velocity of the particle when its acceleration becomes zero is?
View SolutionThree particles start from origin at the same time: one with velocity v1 along positive x-axis, the second along the positive y-axis with a velocity v2 and the third along the line y = x with such a speed that all the three always stay in a straight line, then velocity of the third particles is:
View Solution
