A particle is kept at rest at the origin. A constant force → F starts acting on it at t=0. Find the speed of the particle at time t.
The equation of motion is . →dpdt=→F
As the particle starts from rest and the force is always in the same direction, the motion will be along this direction , Thus, we can write dpdt=F
or, (∫P0dp=∫t0Fdt)
p=Ft
or, m0V√1−v2c2=Ft
or, m20V2=F2t2−F2t2C2V2
V^(2) (m_(0)^(2) + F^(2) t^(2) / C^(2)) = F^(2) t^(2)<br>or,V = Ftc / (sqrt m_(0) ^(2) C^(2) + F^(2) t^(2))
Note from example (47.4) that however large t may be , V can never exceed c, No matter how long you apply a force , the speed of a particl will be less than the speed c.
Topper's Solved these Questions
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMACHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - worked out example
8 Videos
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMACHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Objective
7 Videos
- THE NUCLEOUSBOOK - HC VERMACHAPTER - THE NUCLEOUSEXERCISE - Exercises
53 Videos
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBOOK - HC VERMACHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Exercises
24 Videos
Similar Questions
A particle is kept at rest at the origin. A constant force →F starts acting on it at t=0. Find the speed of the particle at time t.
View SolutionTwo particles are shown in figure. At t=0 a constant force F=6N starts acting on 3kg. Find the velocity of circle of mass of these particle at t=5s.
 .
.
View Solution
Knowledge Check
Two particles are shown in figure. At t=0 a constant force F=6N starts acting on 3kg. Find the velocity of circle of mass of these particle at t=5s.
 .A5m/sB4m/sC6m/sD3m/s
.A5m/sB4m/sC6m/sD3m/sA particle is resting over a smooth horizontal floor AT t = 0, a horizontal force starts acting on it. Magnitude of the force increases with time F = kt, where k is a constant. The two curves are drawn for this particle as shown
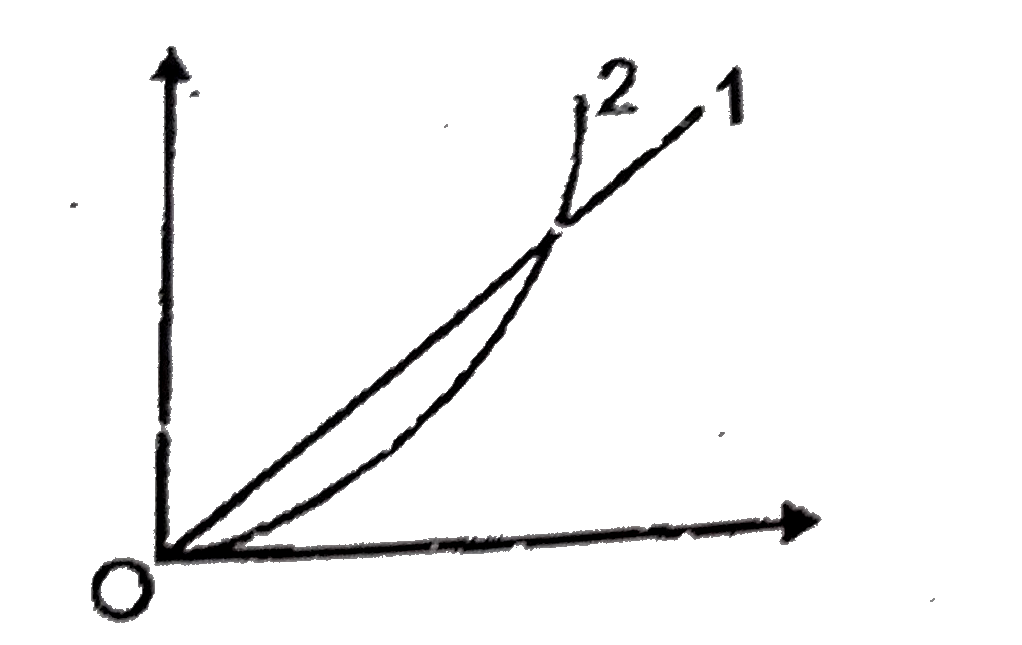 ACurve-1 shows acceleration versus timeBCurve-2 shows velocity versus timeCCurve-2 shows velocity versus accelerationDCurve-1 shows velocity versus acceleration
ACurve-1 shows acceleration versus timeBCurve-2 shows velocity versus timeCCurve-2 shows velocity versus accelerationDCurve-1 shows velocity versus accelerationA graph of acceleration versus time of a particle starting from rest at t =0 is shown. The speed of the particle at t=14 second is
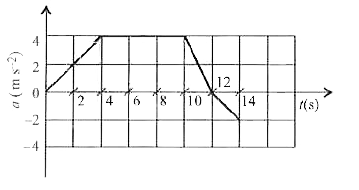 A2ms−1B34ms−1C20ms−1D42ms−1
A2ms−1B34ms−1C20ms−1D42ms−1
A particle can move along a straight line. It is at rest when a force (F) starts acting on it directed along the line. Work done by the force on the particle changes with time(t) according to the graph shown in the fig. Can you say that the force acting on the particle remains constant with time?
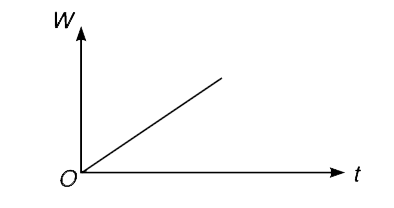
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionA particle starts from rest at time t=0 and moves on a straight line with acceleration as plotted in fig. The speed of the particle will be maximum after time.

View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionA particle is resting over a smooth horizontal floor. At t=0, a horizontal force starts acting on it. Magnitude of the force increases with the time according to law F=at, where 'a' is a constant. For figure which of the following statement is/are correct ?

View Solution
