A particle is moveint along the x-axis whose instantaneous speed is given by v2=108−9x2. The acceleration of the particle is.
−9xms−2
−18xms−2
−9x2ms−2
None of there
The correct Answer is:A
v2=18−9x2
a=dvdt=dvdx.dxdt=d(√108−9x2)dx.dxdt
a=1(−18x)2√108−9x2.√108−9x2=−9x−2
Alternative: Differentiating w.r.t. we get
2vdvdx=−18x
vdxdx=−9x⇒a=−9x∵(vdvdx=a).
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept17videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Graphical cancept1videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Subjective29videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
(a) A particle is moving along the x axis and its velocity vs position graph is as shown. Is the acceleration of the particle increasing, decreasing or remains constant?
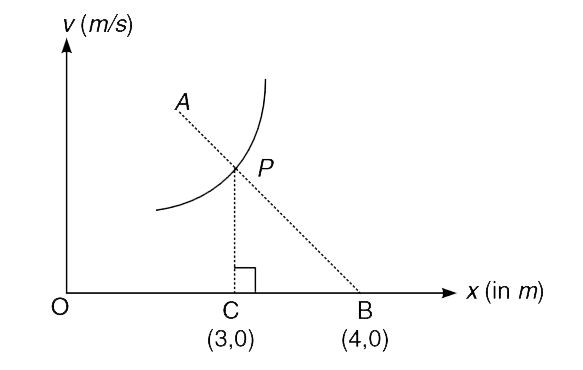
(b) A particle is moving along x axis and its velocity (v) vs position (x) graph is a curve as shown in the figure. Line APB is normal to the curve at point P. Find the instantaneous acceleration of the particle at x=3.0m.
 View Solution
View SolutionThe displacement x of a particle along the x-axis at time t is given by x=a12t+a23t2. Find the acceleration of the particle.
View Solution
Knowledge Check
- Question 1 - Select One
A particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
AzeroB42 mCInfiniteDNone of these - Question 2 - Select One
The potential energy of a 1kg particle free to move along the x-axis is given by V(x)=(x44−x22)J The total mechanical energy of the particle is 2J then the maximum speed (∈m/s) is
A3√2B3√2C92D2 - Question 3 - Select One
A particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
AThe maximum displacement of the particle from the starting point is u√bBThe particle will oscillate about the originCVelocity is maximum at the originDGiven data is insufficient to determine the exact motion of the particle.
A particle is moving along x-axis whose position is given by x=4-9t+(1)/(3) .Mark the correct statements in relation to its motion
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionVelocity of particle moving along x-axis is given as v=(x3−x2+2) m/sec. Find the acceleration of particle at x=2 meter.
View SolutionThe PE of a 2 kg particle, free to move along x-axis is given by V(x)=(x33−x22)J. The total mechanical energy of the particle is 4 J. Maximum speed (in ms−1) is
View SolutionThe potential energy of a 1 kg particle free to move along the x-axis is given by
V(x)(x44−x22)J
The total mechanical energy of the particle is 2 J. Then, the maximum speed (in m/s) isView Solution

