A particle is moving in a straight line along the positive x-axis such that its speed is inversely proportional to the distance from origin [v∝1ξmpliesv=kx where k is the proportionally constant].
The graph of motion of the particle for 1/v versus x (distance from origin) is shown in the figure.
![A particle is moving in a straight line along the positive x-axis such that its speed is inversely proportional to the distance from origin [vprop1/ximpliesv=k/x where k is the proportionally constant]. The graph of motion of the particle for 1//v versus x (distance from origin) is shown in the figure.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/MPP_PHY_C02_S01_110_Q01.png)
The time interval of motion from point A to point B is 12.50
The time interval of motion from point A to point B is 18.75s.
The proportionality constant k is 10m2/s
The proportionality constant k is 20m2/s
The correct Answer is:B, C
Step by step video, text & image solution for A particle is moving in a straight line along the positive x-axis such that its speed is inversely proportional to the distance from origin [vprop1/ximpliesv=k/x where k is the proportionally constant]. The graph of motion of the particle for 1//v versus x (distance from origin) is shown in the figure. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - MATCH THE COLUMN
10 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
A particle moving in straight line,1v versus displacement graph is shown in figure. Find average speed of particle for given 4 m.
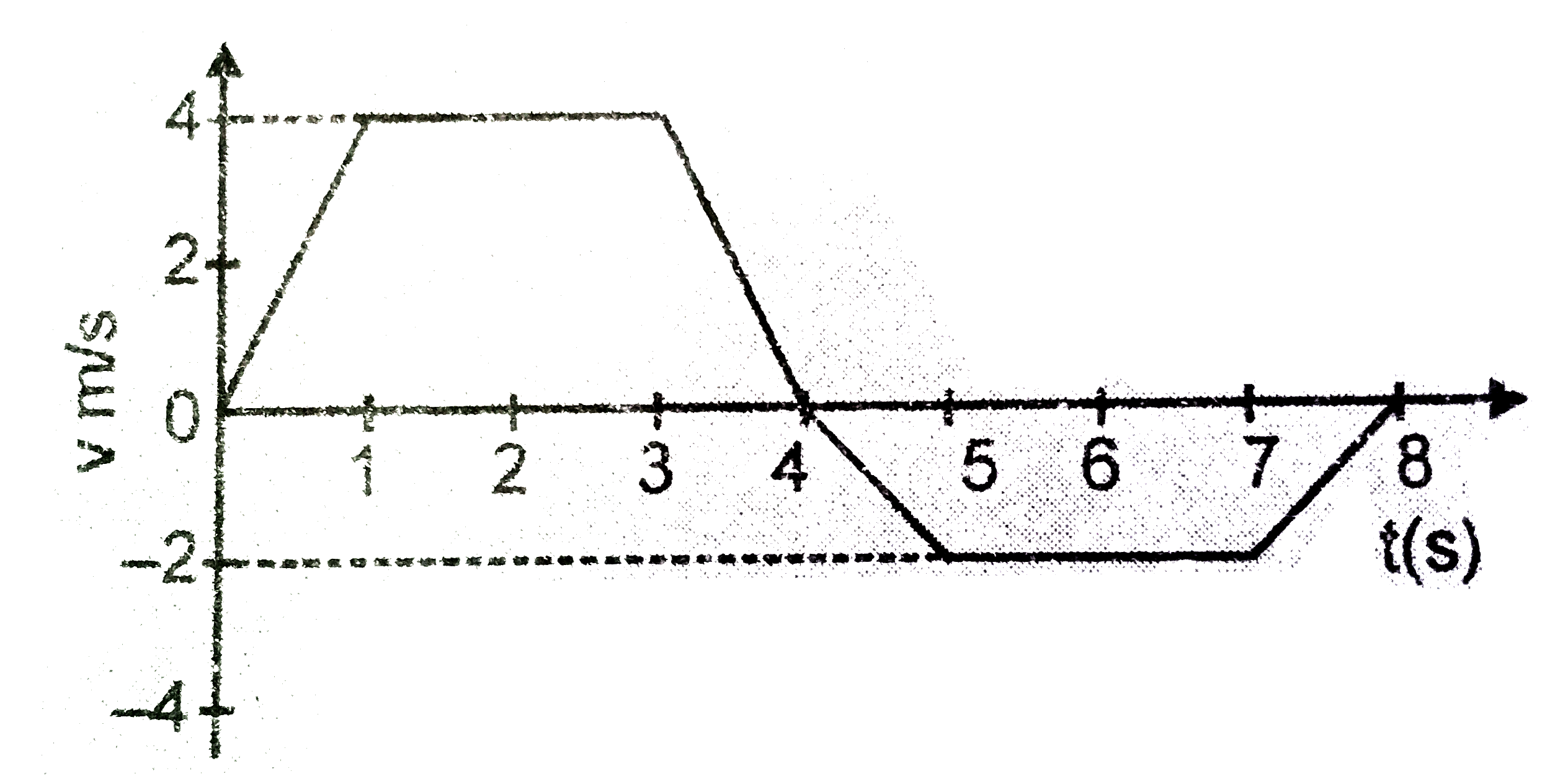
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
View Solution
Knowledge Check
A particle is moving along a straight line parallel to x-axis with constant velocity. Its angular momentum about the origin
Adecreases with timeBincreases with timeCremains constantDis zeroA particle is moving on a straight line such that square of its velocity is directly proportional to distance as shown in graph. What is the acceleration of the particle ?
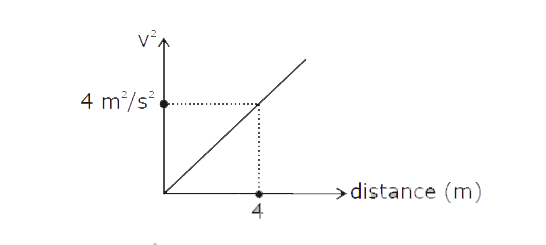 A14m/s2B1m/s2C2m/s2D12m/s2
A14m/s2B1m/s2C2m/s2D12m/s2A particle is moving with speed v=b√x along positive x-axis. Calculate the speed of the particle at time t=τ (assume that the particle is at origin at t = 0).
Ab2τ√2Bb2τ4Cb2τ2Db2τ
A particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
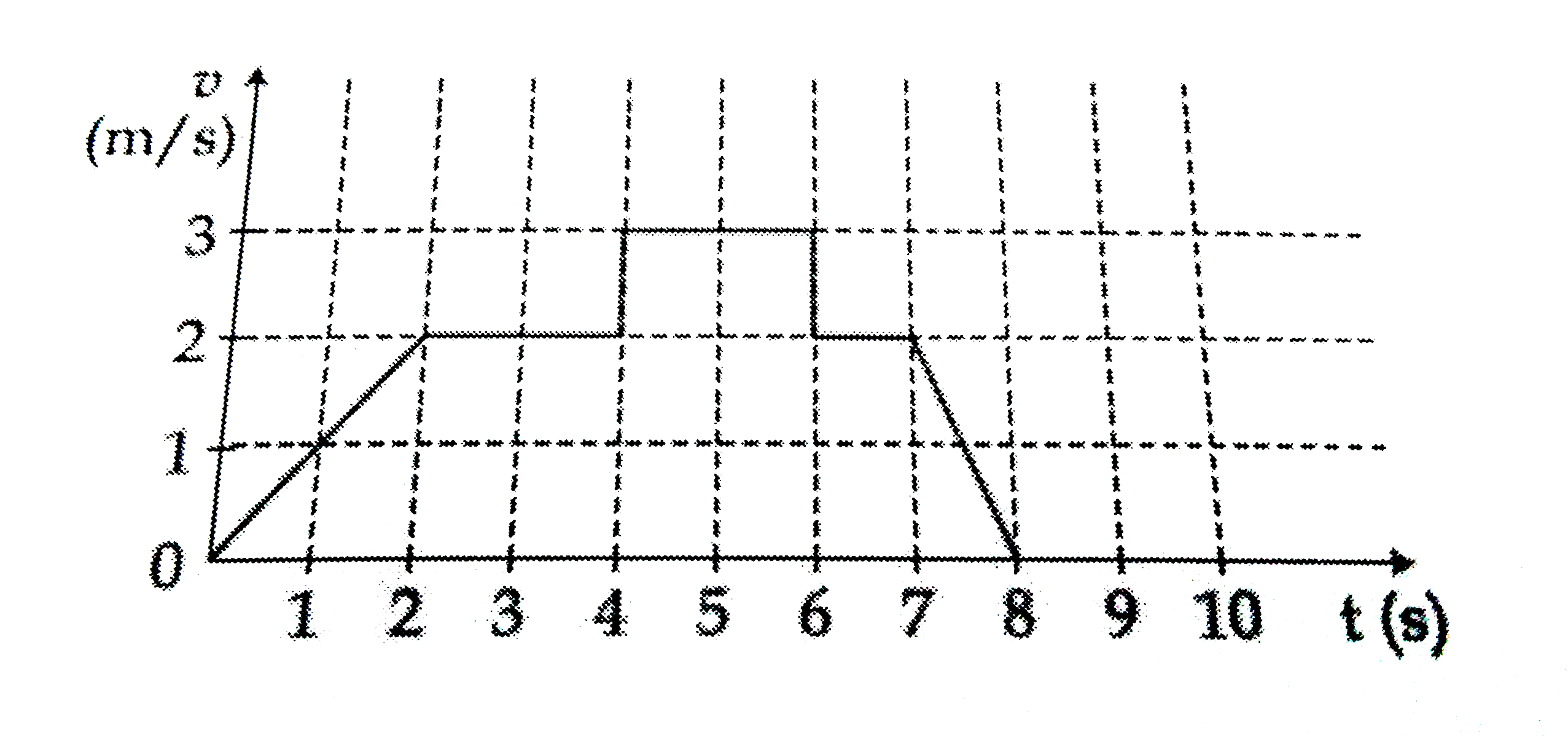
View SolutionA particle is projected with velocity v0 along x - axis. The deceleration on the particle is proportional to the square of the distance from the origin i.e. a=−x2. The distance at which particle stops is -
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (1):
View SolutionA particle is projected with velocity V0along axis x . The deceleration on the particle is proportional to the square of the distance from the origin i.e., a=ωx2.distance at which the particle stops is
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (3) :
View Solution
