A particle is moving in x-y plane. Its initial velocity and acceleration are u=(4ˆi+8ˆj)m/sanda=(2ˆi−4ˆj)m/s2. Find
(a) the time when the particle will cross the x-axis.
(b) x-coordinate of particle at this instant.
(c) velocity of the particle at this instant.
Initial coordinates of particle are (4m,10m).
The correct Answer is:B, D
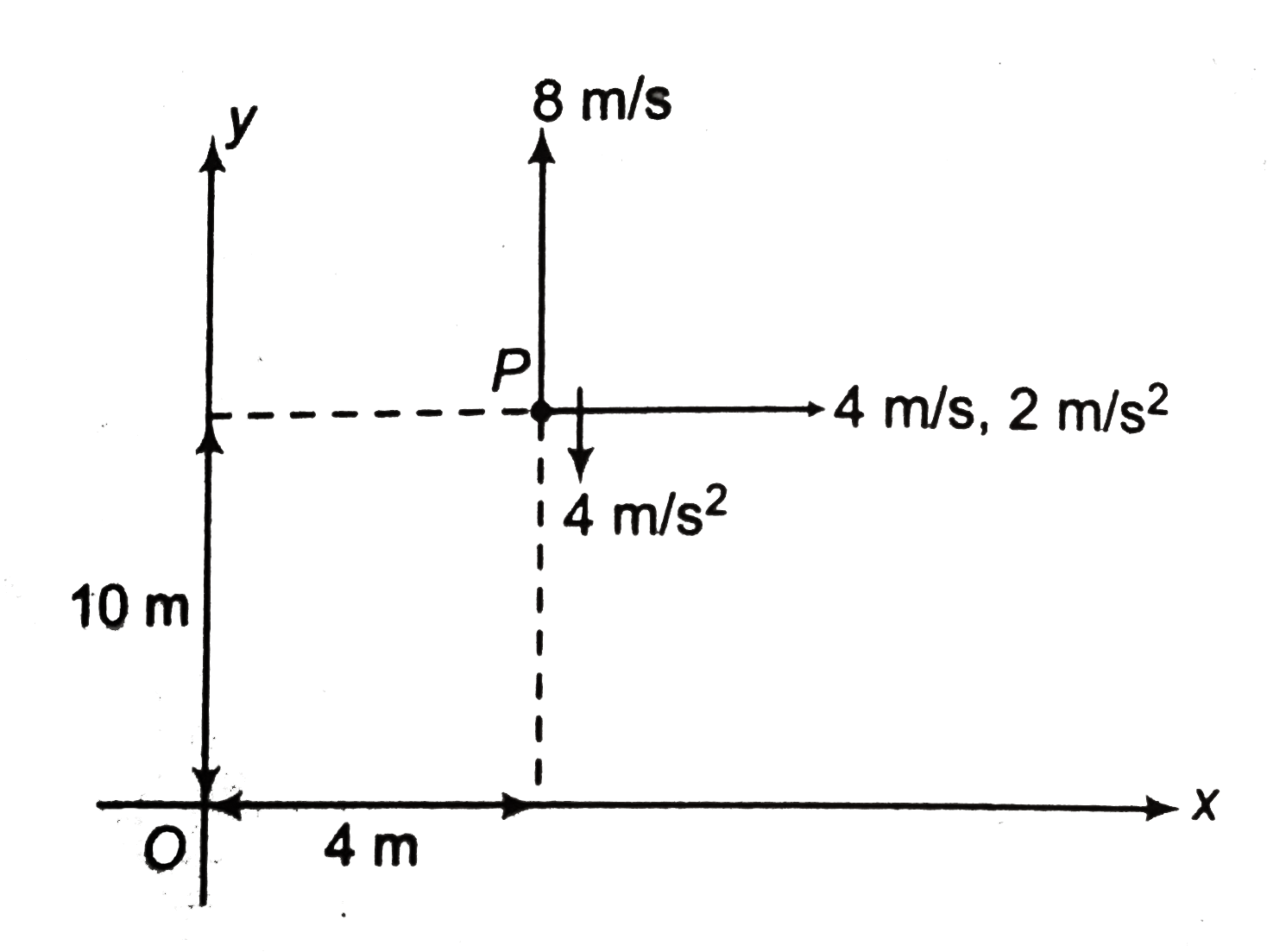
Particle starts from point P. Components of its initial velocity and acceleration are as shown in
figure.
(a) At the time of crossing the x-axis, its y-coordinate should be zero or its y-displacement
(w.r.t initial point P) is −10m.
Using the equation, sy=uyt+12ayt2
−10=8t−12×4×t2
Solving this equation, we get positive value of time,
t=5s
(b) x-coordinate of particle at time t:
x=initial x-coordinate +displacement along x-axis or x=xi+sx (at time t)
=xi+uxt+12axt2
Substuting the proper values, we have,
x=4+(4×5)+12×2×(5)2=49m
(c) Since, given acceleration is constant, so we can use,
v=u+at
∴v=(4ˆi+8ˆj)+(2ˆi−4ˆj)(5)
=(14ˆi−12ˆj)m/s
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 5
1 Video
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 6
1 Video
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 3
1 Video
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Knowledge Check
A particle has an initial velocity 3ˆi+4ˆj and an accleration of 0.4ˆi+0.3ˆj. Its speed after 10s is
A10 unitB7 unitsC7√2 unitsD8.5 unitsA particle has an initial velocity of 4ˆi+3ˆj and an acceleration of 0.4ˆi+0.3ˆj. Its speed after 10s is
A10 unitsB7 unitsC7√2 unitsD8.5 unitsA particle at origin (0,0) moving with initial velocity u=5msˆj and acceleration 10ˆi+4ˆj. After t time it reaches at position (20,y) then find t & y
At = 2, y = 18Bt = 4, y = 16Ct = 6, y = 12Dt =8, y =10
A particle is moving with initial velocity 1m/s and acceleration a=(4t+3)ms2. Find velocity of particle at t=2sec.
View SolutionVelocity and acceleration of a particle at time t=0are u=(2ˆi+3ˆj)m/sanda=(4ˆi+3ˆj)m/s2 respectively. Find the velocity and displacement if particle at t=2s.
View SolutionA particle is given an initial velocity of →u=(3ˆi+4ˆj)m/s. Acceleration of the particle is →a=(3t2+2tˆj)m/s2. Find the velocity of particle at t=2s.
View SolutionA particle has an initial velocity 3ˆi+4ˆj and an accleration of 0.4ˆi+0.3ˆj. Its speed after 10s is
View SolutionA particle is moving in an isolated x−y plane. At an instant, the particle has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2. At that instant what will be the radius of curvature of its path ?
View Solution