Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
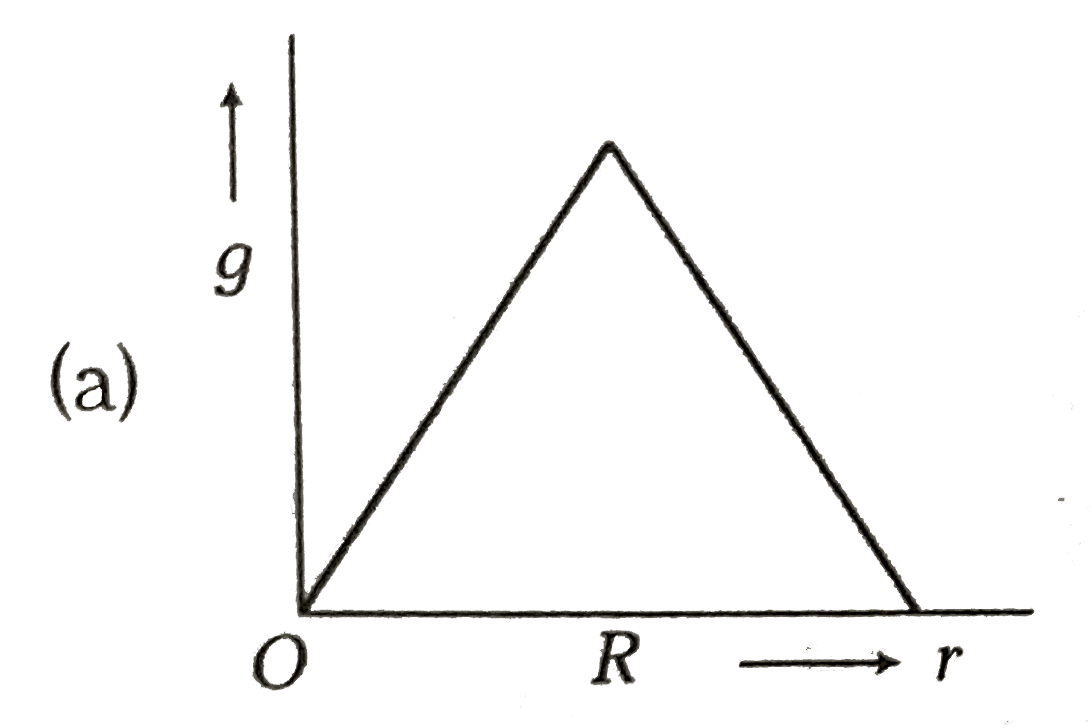
The correct Answer is:B
To determine the variation of acceleration due to gravity (g) starting from the center of the Earth to the surface, we can follow these steps:
Step 1: Understand the formula for g inside the Earth
When we are at a depth d inside the Earth, the acceleration due to gravity g′ can be expressed as:
g′=g(1−dR)
where:
- g is the acceleration due to gravity at the surface of the Earth,
- d is the depth below the surface,
- R is the radius of the Earth.
Step 2: Analyze the relationship
From the formula, we can see that as the depth d increases (moving from the surface to the center of the Earth), the value of g′ decreases linearly. This means that at the center of the Earth (where d=R), g′=0.
Step 3: Plot the variation of g
- At the surface (depth d=0), g′=g.
- As we move towards the center (increasing d), g′ decreases linearly until it reaches 0 at the center (depth d=R).
- The graph of g′ versus d will be a straight line starting from g at d=0 and reaching 0 at d=R.
Step 4: Identify the correct option
Given the linear decrease of g′ with increasing depth, we can conclude that the correct representation of this variation is a straight line that slopes downwards from g to 0.
Conclusion
Thus, the variation of g starting from the center of the Earth to the surface is represented by a linear graph that decreases from g to 0.
When we are at a depth d inside the Earth, the acceleration due to gravity g′ can be expressed as:
g′=g(1−dR)
where:
- g is the acceleration due to gravity at the surface of the Earth,
- d is the depth below the surface,
- R is the radius of the Earth.
From the formula, we can see that as the depth d increases (moving from the surface to the center of the Earth), the value of g′ decreases linearly. This means that at the center of the Earth (where d=R), g′=0.
- At the surface (depth d=0), g′=g.
- As we move towards the center (increasing d), g′ decreases linearly until it reaches 0 at the center (depth d=R).
- The graph of g′ versus d will be a straight line starting from g at d=0 and reaching 0 at d=R.
Given the linear decrease of g′ with increasing depth, we can conclude that the correct representation of this variation is a straight line that slopes downwards from g to 0.
Thus, the variation of g starting from the center of the Earth to the surface is represented by a linear graph that decreases from g to 0.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If g is acceleration due to gravity on the surface of the earth, having radius R, the height at which the acceleration due to gravity reduces to g/2 is
AR/2B√2RCR√2D(√2−1)RAt the centre of earth the acceleration due to gravity is
AinfiniteBzeroC9.8ms−2Dall of theseOne goes from the centre of the earth to a distance two third the radius of the earth. The acceleration due to gravity is highest at
Athe centre of the earthBa distance half the radius of the earthCa distance one-third of the radius of the earthDa distance two-third of the radius of the earth
Starting from the surface of earth, the variation of acceleration due to gravity (g) with height (h) can be represented by
View SolutionObtain an expression for the acceleration due to gravity on the surface of the earth in terms of mass of the earth and its radius. Discuss the variation of acceleration due to gravity with altitude and depth. If a body is taken to a height R / 4 from the surface of the earth, find percentage decrease in the weight of the body ? Here R is the radius of the earth.
View SolutionIf g is acceleration due to gravity on the surface of the earth,having radius R ,the height at which the acceleration due to gravity reduces to g/2 is
View SolutionDoes the concentration of the earth's mass near its centre change the variation of g (acceleration due to gravity) with height from its surface?
View SolutionAt what distance from the centre of the earth, the value of acceleration due to gravity g will be half that on the surface ( R = radius of earth)
View Solution