Question

A particle is moving on a cicular path of radius 'R' . As it moves through an angular displacement ${\displaystyle \theta }$, its linear displacement will be :

Answer

In the foregoing example, find the angle between `vecA` and `vecB`.
'`theta= cos ^(-1){(A_(x) B_(x) + A_(y) B_(y) + A_(z) B_(z))/(sqrt((A_(x)^(2)+A_(y)^(2) + A_(z)^(2))(B_(x)^(2) + B_(y)^(2) + B_(z)^(2))))}`

Explanation

When the insect moves from positon to position 2, the displacement `vecs` = change in position vectors `Deltavecr`.
Since `Delta vecr= vecr_(2) - vecr_(1)`, the magnitude of the displacement is
`|Deltavecr| = sqrt(r_(1)^(2) + r_(2)^(2) - 2r_(1)r_(2) cos theta ).`

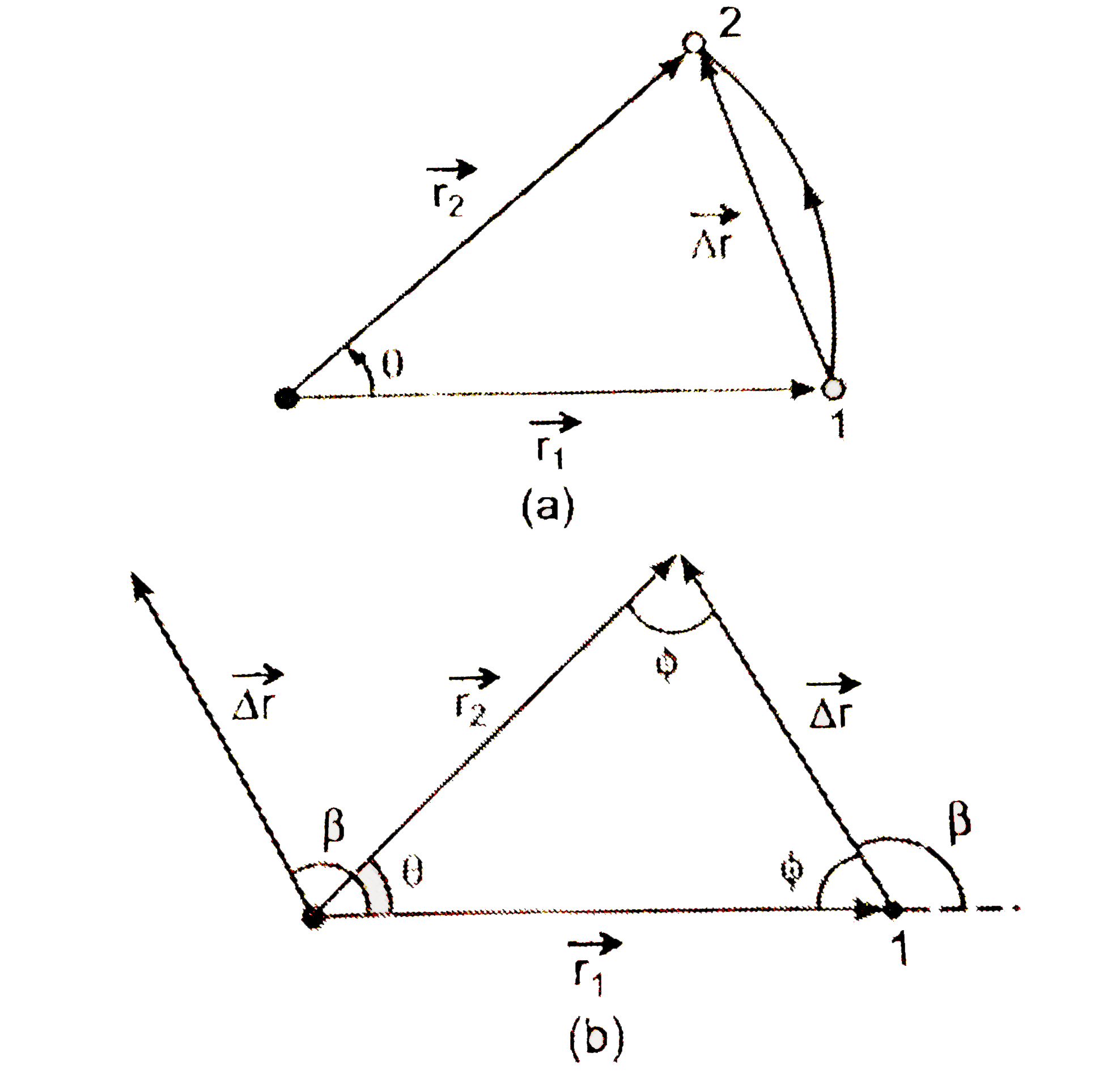
Since the insect moves in a circular path, `r_(1) = r_(2) = R`
Hence `|Deltavecr| = 2 R sin .(theta)/(2)`. The direction of `Deltavecr` is given as
`beta= (pi)/(2) + (theta)/(2)`, as shown in the Fig.3.42 .