A particle is moving with an initial velocity of 2m/s and covers a distance of 20m in 5s. Find (a) acceleration of particle (b) time taken by the particle to attain a velocity of 10m/s.
To solve the problem step by step, we will break it down into two parts as asked: (a) finding the acceleration of the particle and (b) finding the time taken by the particle to attain a velocity of 10 m/s.
Part (a): Finding the Acceleration of the Particle
1. Identify Given Values:
- Initial velocity (u) = 2 m/s
- Distance covered (s) = 20 m
- Time taken (t) = 5 s
2. Use the Second Equation of Motion:
The second equation of motion is given by:
s=ut+12at2
where s is the distance, u is the initial velocity, a is the acceleration, and t is the time.
3. Substitute the Known Values:
Substitute s=20 m, u=2 m/s, and t=5 s into the equation:
20=2(5)+12a(52)
4. Simplify the Equation:
Calculate 2(5):
20=10+12a(25)
This simplifies to:
20=10+25a2
5. Rearrange to Solve for Acceleration (a):
Subtract 10 from both sides:
10=25a2
Multiply both sides by 2:
20=25a
Divide by 25:
a=2025=0.8m/s2
Part (b): Finding the Time Taken to Attain a Velocity of 10 m/s
1. Identify Given Values:
- Initial velocity (u) = 2 m/s
- Final velocity (v) = 10 m/s
- Acceleration (a) = 0.8 m/s² (from part a)
2. Use the First Equation of Motion:
The first equation of motion is given by:
v=u+at
3. Substitute the Known Values:
Substitute v=10 m/s, u=2 m/s, and a=0.8 m/s² into the equation:
10=2+(0.8)t
4. Rearrange to Solve for Time (t):
Subtract 2 from both sides:
8=0.8t
Divide by 0.8:
t=80.8=10s
Final Answers:
(a) The acceleration of the particle is 0.8m/s2.
(b) The time taken by the particle to attain a velocity of 10m/s is 10s.
- Initial velocity (u) = 2 m/s
- Distance covered (s) = 20 m
- Time taken (t) = 5 s
The second equation of motion is given by:
s=ut+12at2
where s is the distance, u is the initial velocity, a is the acceleration, and t is the time.
Substitute s=20 m, u=2 m/s, and t=5 s into the equation:
20=2(5)+12a(52)
Calculate 2(5):
20=10+12a(25)
This simplifies to:
20=10+25a2
Subtract 10 from both sides:
10=25a2
Multiply both sides by 2:
20=25a
Divide by 25:
a=2025=0.8m/s2
- Initial velocity (u) = 2 m/s
- Final velocity (v) = 10 m/s
- Acceleration (a) = 0.8 m/s² (from part a)
The first equation of motion is given by:
v=u+at
Substitute v=10 m/s, u=2 m/s, and a=0.8 m/s² into the equation:
10=2+(0.8)t
Subtract 2 from both sides:
8=0.8t
Divide by 0.8:
t=80.8=10s
(a) The acceleration of the particle is 0.8m/s2.
(b) The time taken by the particle to attain a velocity of 10m/s is 10s.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CONCEPTUAL QUESTIONS
14 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - TOUGH & TRICKY ( PROBLEMS)
10 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
A particle is moving with initial velocity 1m/s and acceleration a=(4t+3)ms2. Find velocity of particle at t=2sec.
View SolutionA particle is moving along a straight line.The initial velocity is 10ms and it is , moving with constant retardation of 2ms2 .. The distance travelled by the particle until it comes to rest is
View Solution
Knowledge Check
A particle is moving with velocity 5 m/s towards cast and its velocity changes to 5 m/s north in 10 s, find the acceleration .
A√2 North- WestB1√2 North - WestC1√2 North - EastD√2 North -EastA particle is moving with velocity 5 m/s towards cast and its velocity changes to 5 m/s north in 10 s, find the acceleration .
A√2 N-WB1√2 N-WC1√2 N-ED√2N−EA particle is moving eastwards with a velocity of 5m/s. In 10s the velocity changes to 5m/s nothwards. The average acceleration in this time is
AZeroB1√2m/s2 towards north-westC12m/s2 towards northD1√2m/s2 towards north-east
A paricle is moving eastwards with a velocity of 5m/s. In 10s the velocity changes to 5m/s northwards. Find the average acceleration in this time.
View SolutionA particle having initial velocity u moves with a constant acceleration a for a time t. a. Find the displacement of the particle in the last 1 second . b. Evaluate it for u=5m/s,a=2m/s2andt=10s.
View SolutionA particle is given an initial velocity of 20m/s. acceleration of the particle changes with time and its variation is shown in the following figure.
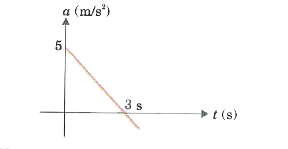
View SolutionA particle is moving eastwards with a velocity of 5m/s. In 10s the velocity changes to 5m/s nothwards. The average acceleration in this time is
View SolutionA particle is projected with an initial velocity of 200m/s in a direction making an angle of 30∘ with the vertical. The horizontal distance covered by the particle in 3s is
View Solution
