The velocity of an object varies as v=ht24. Calculate the change in position of the ball is time t.
To solve the problem of calculating the change in position of an object when its velocity varies as v=ht24, we can follow these steps:
Step 1: Understand the relationship between velocity and position
Velocity is defined as the rate of change of position with respect to time. Mathematically, this is expressed as:
v=dxdt
where dx is the change in position and dt is the change in time.
Step 2: Express the change in position in terms of velocity
From the definition of velocity, we can express the change in position dx as:
dx=vdt
Substituting the given expression for velocity:
dx=ht24dt
Step 3: Integrate to find the change in position
To find the total change in position over a time interval from 0 to t, we need to integrate dx:
Δx=∫t0ht24dt
Since h is a constant, we can take it out of the integral:
Δx=h4∫t0t2dt
Step 4: Perform the integration
The integral of t2 is:
∫t2dt=t33
Now, applying the limits from 0 to t:
Δx=h4(t33−033)
This simplifies to:
Δx=h4⋅t33=ht312
Step 5: State the final result
Thus, the change in position of the ball at time t is:
Δx=ht312
Velocity is defined as the rate of change of position with respect to time. Mathematically, this is expressed as:
v=dxdt
where dx is the change in position and dt is the change in time.
From the definition of velocity, we can express the change in position dx as:
dx=vdt
Substituting the given expression for velocity:
dx=ht24dt
To find the total change in position over a time interval from 0 to t, we need to integrate dx:
Δx=∫t0ht24dt
Since h is a constant, we can take it out of the integral:
Δx=h4∫t0t2dt
The integral of t2 is:
∫t2dt=t33
Now, applying the limits from 0 to t:
Δx=h4(t33−033)
This simplifies to:
Δx=h4⋅t33=ht312
Thus, the change in position of the ball at time t is:
Δx=ht312
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CONCEPTUAL QUESTIONS
Explore 14 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:TOUGH & TRICKY ( PROBLEMS)
Explore 10 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Practice Test (For Board Examination)
Explore 12 Videos
Similar Questions
An object is moving along +ve x-axis with a uniform acceleration of 4ms−2 . At time t=0 , x=5m and v=3ms−1 .
(a) What will be the velocity and position of the object at time t=2s?
What will be the velocity and position of the object when it has a velocity of 5ms−1?
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View SolutionInstantaneous velocity of an object varies with time as v=α−βt2. Find its position and acceleration as a function of time, also find the object's maximum positive displacement from the origin.
View SolutionIf the relation between acceleration and time for an object is given by
a=2t+4t2
Calculate the position of object from the origin at t = 4 s. Assume the object to be at rest at t=0.
View SolutionAn object is moving along+ve x-axis with a uniform acceleration of 4 ms^(-2).Attime t=0.X=4m and v=2ms−1.<br>(a)Wˆwillbethevelocityandpositionoftheobjectattime t=3 s?
(b) What will be the position of the object when it has a velocity 8ms−1 ?
View SolutionVelocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View SolutionThe velocity of an object is changing with time and relation is given by the following equation.
v=2t+3t2
Calculate the position of the object from the origin at t = 2 s.
Assume particle to be at origin at t = 0
View SolutionThe velocity of an object is changing with time and relation is given by the following equation.
v=2t+3t2
Calculate the position of the object from the origin at t=2s.
View SolutionThe acceleration of a particle varies with time as shown in .
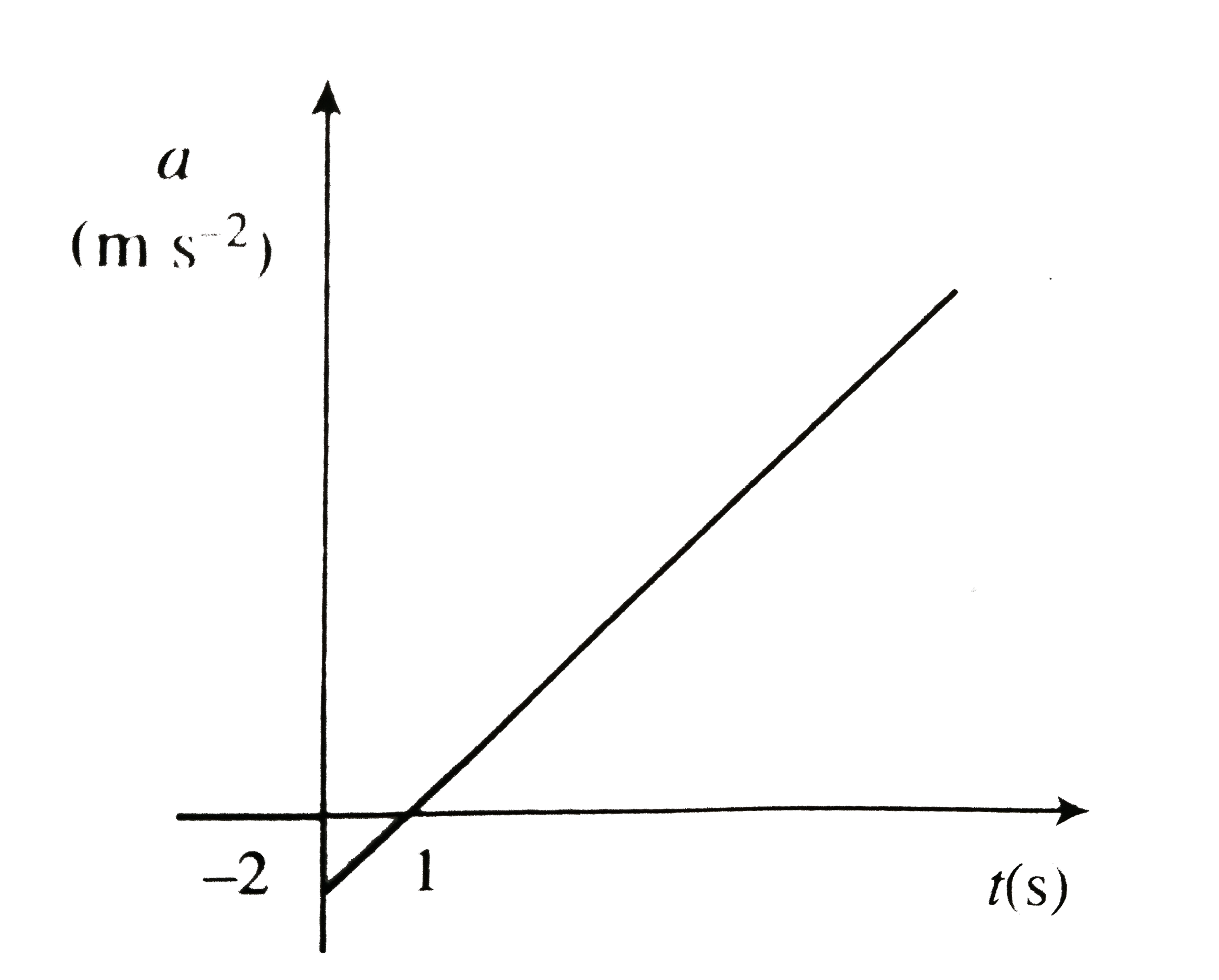 .
.
a. Find an expression for velocityinterms of t. Assume that v=0 at t=0
b. Calculate the displacement of the paarticle in the time interval from t=2s s.
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View Solution
