A particle is projected along a horizontal field whose coefficient of friction varies as μ=A/r2, where r is the distance from the origin in meters and A is a positive constant. The initial distance of the particle is 1m from the origin and its velocity is radially outwards. The minimum initial velocity at this point so the particle never stops is
(a) ∞
(b) 2√gA
(c) √2gA
(d) 4√gA
The correct Answer is:C
To solve the problem, we will use the work-energy theorem, which states that the work done by all forces acting on a particle is equal to the change in its kinetic energy.
1. Identify the Forces Acting on the Particle:
The only force acting on the particle in this scenario is the frictional force, which opposes the motion. The coefficient of friction is given as μ=Ar2.
2. Set Up the Work-Energy Theorem:
According to the work-energy theorem:
Wtotal=ΔKE
where Wtotal is the work done by friction and ΔKE is the change in kinetic energy.
3. Calculate the Work Done by Friction:
The work done by friction can be expressed as:
Wfriction=−∫∞1μ⋅mgdx
Substituting μ:
Wfriction=−∫∞1Ax2mgdx
4. Evaluate the Integral:
The integral simplifies to:
Wfriction=−mgA∫∞11x2dx
The integral ∫1x2dx evaluates to −1x, so:
Wfriction=−mgA(−1x)∞1=−mgA(0+1)=−mgA
5. Determine the Change in Kinetic Energy:
The initial kinetic energy KEi is given by:
KEi=12mu2
The final kinetic energy KEf is 0 since the particle stops at infinity. Thus:
ΔKE=KEf−KEi=0−12mu2=−12mu2
6. Apply the Work-Energy Theorem:
Setting the work done by friction equal to the change in kinetic energy:
−mgA=−12mu2
We can cancel m from both sides (assuming m≠0):
gA=12u2
7. Solve for the Initial Velocity u:
Rearranging gives:
u2=2gA
Taking the square root:
u=√2gA
Final Answer:
The minimum initial velocity u at the point where the particle is 1 meter from the origin so that it never stops is:
u=√2gA
The only force acting on the particle in this scenario is the frictional force, which opposes the motion. The coefficient of friction is given as μ=Ar2.
According to the work-energy theorem:
Wtotal=ΔKE
where Wtotal is the work done by friction and ΔKE is the change in kinetic energy.
The work done by friction can be expressed as:
Wfriction=−∫∞1μ⋅mgdx
Substituting μ:
Wfriction=−∫∞1Ax2mgdx
The integral simplifies to:
Wfriction=−mgA∫∞11x2dx
The integral ∫1x2dx evaluates to −1x, so:
Wfriction=−mgA(−1x)∞1=−mgA(0+1)=−mgA
The initial kinetic energy KEi is given by:
KEi=12mu2
The final kinetic energy KEf is 0 since the particle stops at infinity. Thus:
ΔKE=KEf−KEi=0−12mu2=−12mu2
Setting the work done by friction equal to the change in kinetic energy:
−mgA=−12mu2
We can cancel m from both sides (assuming m≠0):
gA=12u2
Rearranging gives:
u2=2gA
Taking the square root:
u=√2gA
The minimum initial velocity u at the point where the particle is 1 meter from the origin so that it never stops is:
u=√2gA
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A particle is projected from origin x-axis with velocity V0 such that it suffers retardation of magnitude given by Kx3 (where k is a positive constant).The stopping distance of particle is
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View Solution
Knowledge Check
A particle starts from point A moves along a straight line path with an acceleration given by a = p - qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
ApqBp√qCqpD√qp
A large number of particles are placed around the origin, each at a distance R from the origin. The distance of the center of mass of the system from the origin is
View SolutionAll the particles of a body are situated at a distance R from the origin. The distance of the centre of mass of the body from the origin is
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
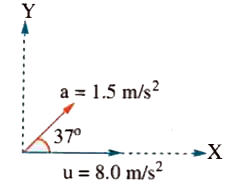
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA particle is projected with velocity v0 along x - axis. The deceleration on the particle is proportional to the square of the distance from the origin i.e. a=−x2. The distance at which particle stops is -
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View SolutionA particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
View SolutionAll the particles of a body situated at distance R from the origin. The distance of the center of mass of the body from the origin is
View Solution
