A particle A of mass 10/7kg is moving in the positive direction of x-axis. At initial position x=0, its velocity is 1ms−1, then its velocity at x=10m is (use the graph given)

(a) 4ms−1
(b) 2ms−1
(c) 3√2ms−1
(d) 1003ms−1
The correct Answer is:A
Area under P−x graph
=∫pdx=(mdvdt)vdx=v∫1mv2dV
=[mv33]v1=107×3(v3−1)
From the graph, area=12(2+4)×10=30
or 107×3(v3−1)=30
or v=4ms−1
Alternative method:
From graph
P=0.2x+2
mvdvdxv=0.2x+2
mv2dv=(0.2x+2)dx
Now integrating both sides, we get
v∫1mv2dv=10∫0(0.2x+2)dx
v=4ms−1
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension55videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective23videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A particle of mass 10−2kg is moving along the positive x axis under the influence of a force F(x)=−K/(2x2) where K=10−2Nm2. At time t=0 it is at x=1.0m and its velocity is v=0.
(a) Find its velocity when it reaches x=0.50m.
(b) Find the time at which it reaches x=0.25m.View SolutionThe velocity of a particle moving in the positive direction of x-axis veries as v=10√x. Assuming that at t=0, particle was at x=0
View SolutionA particle of mass 1031kg is moving with a velocity equal to 105ms−1. The wavelength of the particle is equal to
View SolutionA particle of mass m1 moving with velocity v in a positive direction collides elastically with a mass m2 moving in opposite direction also at velocity v. If m2>>m1, then
View SolutionA particle moving in the positive x-direction has initial velocity v0. The particle undergoes retardation kv2 , where vis its instantaneous velocity. The velocity of the particle as a function of time is given by:
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V-t graph.
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
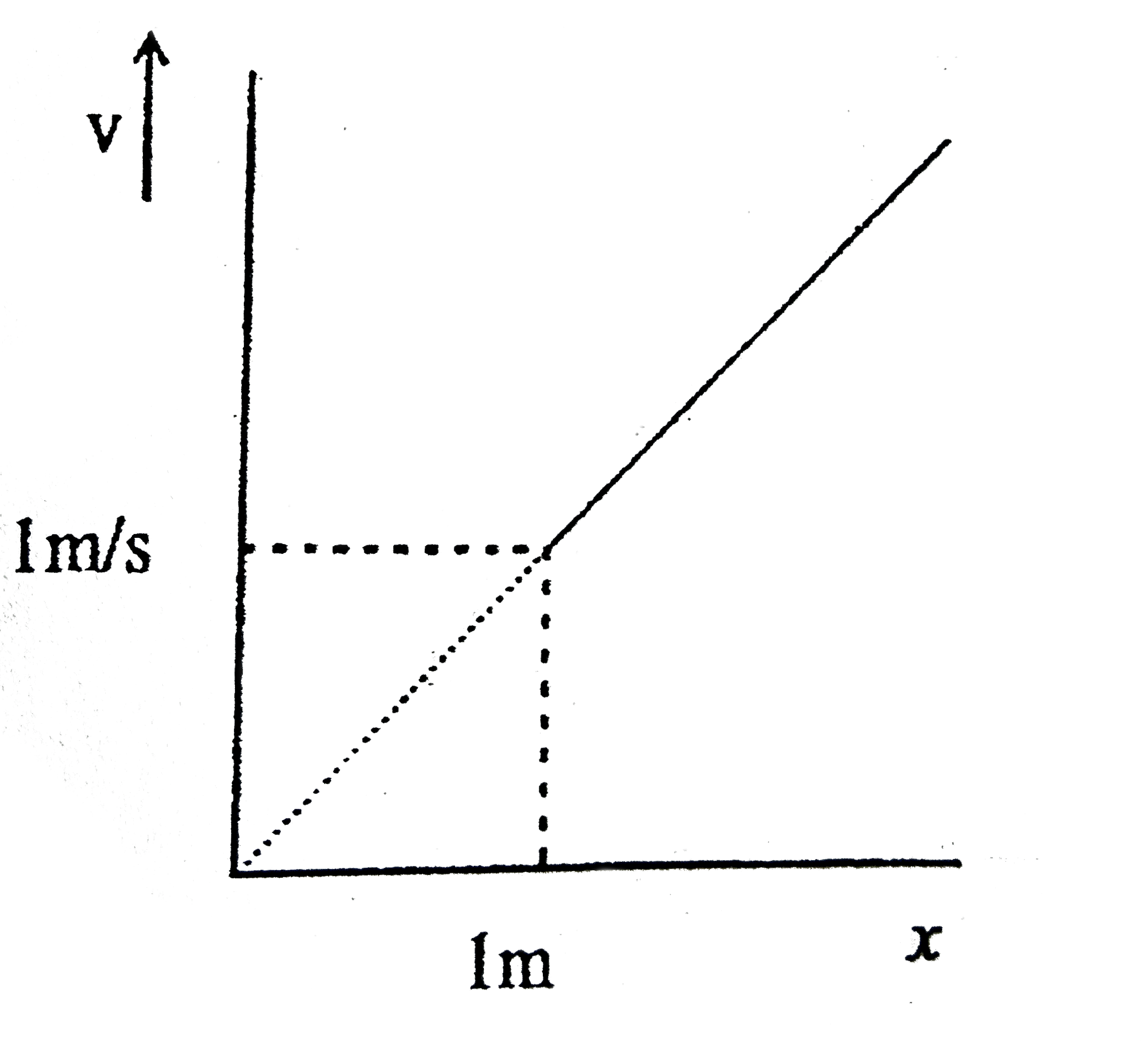 View Solution
View SolutionThe acceleration of a particle which moves along the positive x-axis varies with its position as shown in figure. If the velocity of the particle is 0.8ms−1 at x = 0, then velocity of the particle at x=1.4m is (∈ms−1).
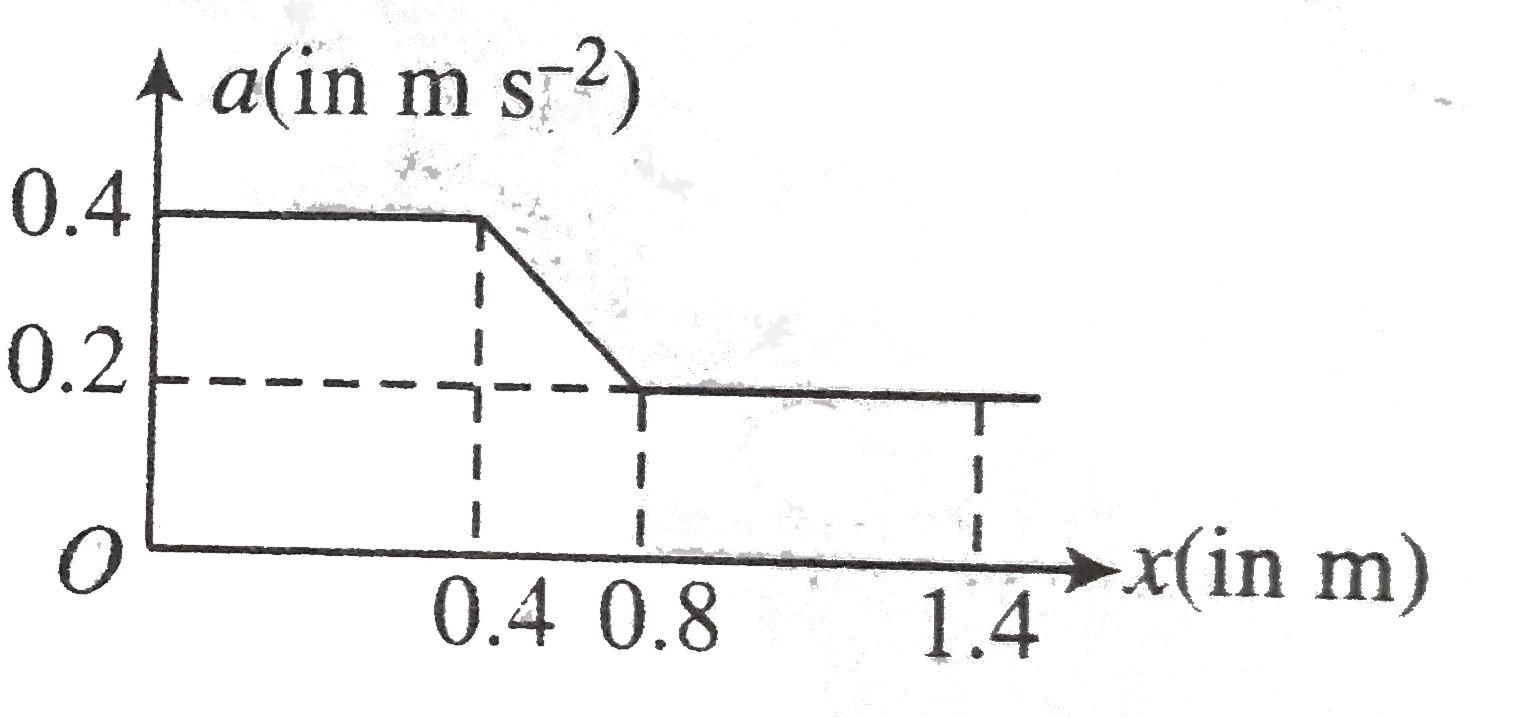 View Solution
View SolutionA particle is moving along x-direction with a constant acceleration a. The particle starts from x=x0 position with initial velocity u. We can define the position of the particle with time by the relation
x=x0+ut+12at2
plot the position of the particle in relation with time is following situations
(i) If initial position of the particle is on negativ x-axis, initial velocity is positive and acceleration is negative.
(ii) If initial position is positive, initial velocity is negative and acceleration is positive.View SolutionA ball of mass 200g is moving with a velocity of 10msec−1 . If the error in measurement of velocity is 0.1%, the uncertainty in its position is :
View Solution

