A particle is projected from ground at some angle with the horizontal. Let $P$ be the point at maximum height $H$ . At what height above the point $P$ should the particle be aimed to have equal to maximum height ?

A

H

B

2 H

C

H//2

D

3 H

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

(a) $A C = R / 2, P C = H$
We have to find $h = M P$ .
From the figure in previous question, we know that if $H = R$ , then
$\tan θ = 4$
Now $\tan θ = \frac{M C}{A C} = \frac{M P + P C}{A C}$
$4 = \frac{h + H}{R / 2} \Rightarrow 4 = \frac{(h + H) 2}{H} \Rightarrow h = H$ .
.

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

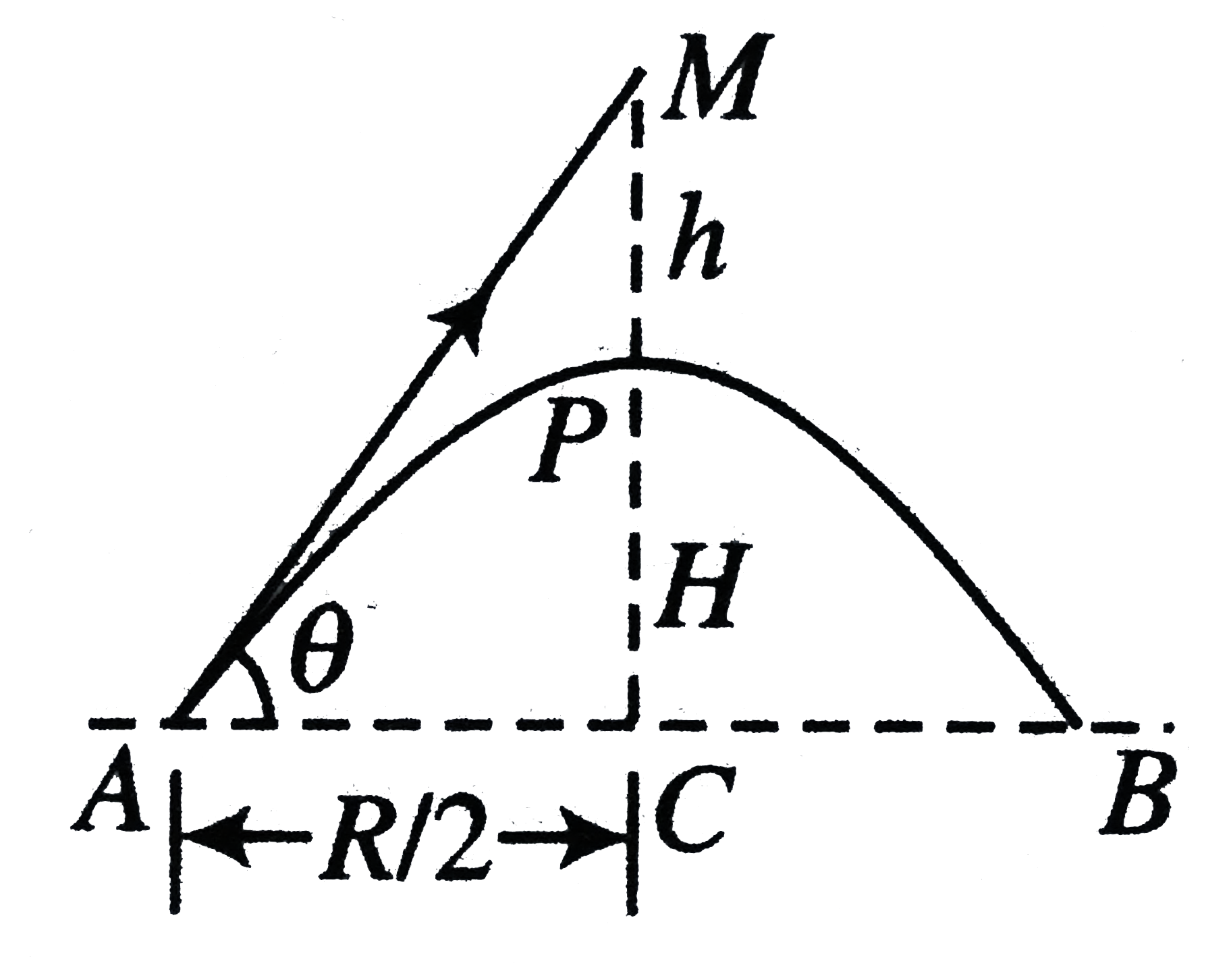Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Particle is projected from the ground at a certain angle with horizontal . If particle takes time T to hit the ground again , then maximum height of the projectile is
A $\frac{T^{2} g}{2}$
B $\frac{T^{2} g}{4}$
C $\frac{T^{2} g}{8}$
D $\frac{T^{2} g}{5}$
Question 2 - Select One
A particle is projected from ground at an angle $θ$ with horizontal with speed u. The ratio of radius of curvature of its trajectory at point of projection to radius of curvature at maximum height is -
A $\frac{1}{{sin}^{2} θ cos θ}$
B ${cos}^{2} θ$
C $\frac{1}{{sin}^{3} θ}$
D $\frac{1}{{cos}^{3} θ}$
Question 3 - Select One
A particle is projected from ground with speed u and at an angle $θ$ with horizontal. If at maximum height from ground, the speed of particle is $1 / 2$ times of its initial velocity of projection, then find its maximum height attained.
A $\frac{u^{2}}{g}$
B $\frac{2 u^{2}}{g}$
C $\frac{u^{2}}{2 g}$
D $\frac{3 u^{2}}{8 g}$

CENGAGE PHYSICS-KINEMATICS-2-Exercise Single Correct

Home
Ask Doubt
Profile