A particle of mass m is projected with a velocity v making an angle of 45° with the horizontal. The magnitude of the angular momentum of the projectile about the point of projection, when the particle is at its maximum height h, is

A

zero

B

$\frac{m v^{3}}{4 \sqrt{2} g}$

C

$\frac{m v^{3}}{\sqrt{2} g}$

D

$m \sqrt{2 g h^{3}}$

Text Solution

Verified by Experts

The correct Answer is:B, D

About a given point, angular momentum = moment of linear momentum
Height of a projectile= h

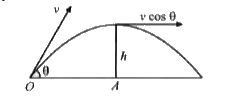
$∴ h = \frac{v^{2} {sin}^{2} θ}{2 g} = \frac{v^{2} \times {sin}^{2} 45^{\circ}}{2 g} = \frac{v^{2}}{4 g}$ ….(i)
At maximum height, the velocity of projectile
$v cos θ = v {cos 45}^{\circ} = \frac{v}{\sqrt{2}}$
$∴$ Momentum at highest point $= \frac{m v}{\sqrt{2}}$
$∴$ Moment of momentum about point O $= \frac{m v}{\sqrt{2}} \times h$
$∴$ Angular momentum about O = $\frac{m v h}{\sqrt{2}}$
$∴ L = \frac{m v h}{\sqrt{2}}$ ...(ii)
Put h from (i) in (ii), we get,
$L = \frac{m v}{\sqrt{2}} \times (\frac{v^{2}}{4 g}) = \frac{m v^{3}}{4 \sqrt{2} g}$ ...(iii)
From (i), eliminate v in (iii)
Angular momentum $= \frac{m v^{3}}{4 \sqrt{2} g} = \frac{m \times {(4 g h)}^{3 / 2}}{4 \sqrt{2} g}$
or $L = m \sqrt{2 g h^{3}}$ ...(iv)
Options (b, d) represent the answers.

|

Updated on:21/07/2023

Class 12 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass 'm' is projected with a velocity $υ$ making an angle of $30^{\circ}$ with the horizontal. The magnitude of angular moment of the projectile about the point of projection when the particle is at its maximum height 'h' is
A $\frac{\sqrt{3}}{2} \frac{m υ^{2}}{g}$
Bzero
C $\frac{m υ^{3}}{\sqrt{2} g}$
D $\frac{\sqrt{3}}{2} \frac{m υ^{2}}{g}$
Question 2 - Select One
A rigid body of moment of inertial $I$ is projected with velocity $V$ making an angle of $45^{\circ}$ with horizontal. The magnitude of angular momentum of the projectile about the point of projection when the body is its maximum height is given by $\frac{I V^{3}}{2 \sqrt{2} g R^{2}}$ where $R$ is the radius of the rigid body. the ridid body is
Asphere
Bspherical shell
Cdisc
Dnone of these
Question 3 - Select One
A particle of mass m is projected with a velocity $μ$ at an angle of $θ$ with horizontal.The angular momentum of the particle about the highest point of its trajectory is equal to :
A $\frac{{mu}^{3} {sin}^{2} θ cos θ}{3 g}$
B $\frac{3 {mu}^{3} {sin}^{2} θ cos θ}{3 g}$
C $\frac{{mu}^{3} {sin}^{2} θ cos θ}{2 g}$
D $\frac{2 {mu}^{3} sin θ {cos}^{2} θ}{3 g}$

MTG-WBJEE-MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTION-WB-JEE WORKOUT (CATEGORY 2 : Single Option Correct Type (2 Marks))

Home
Ask Doubt
Profile