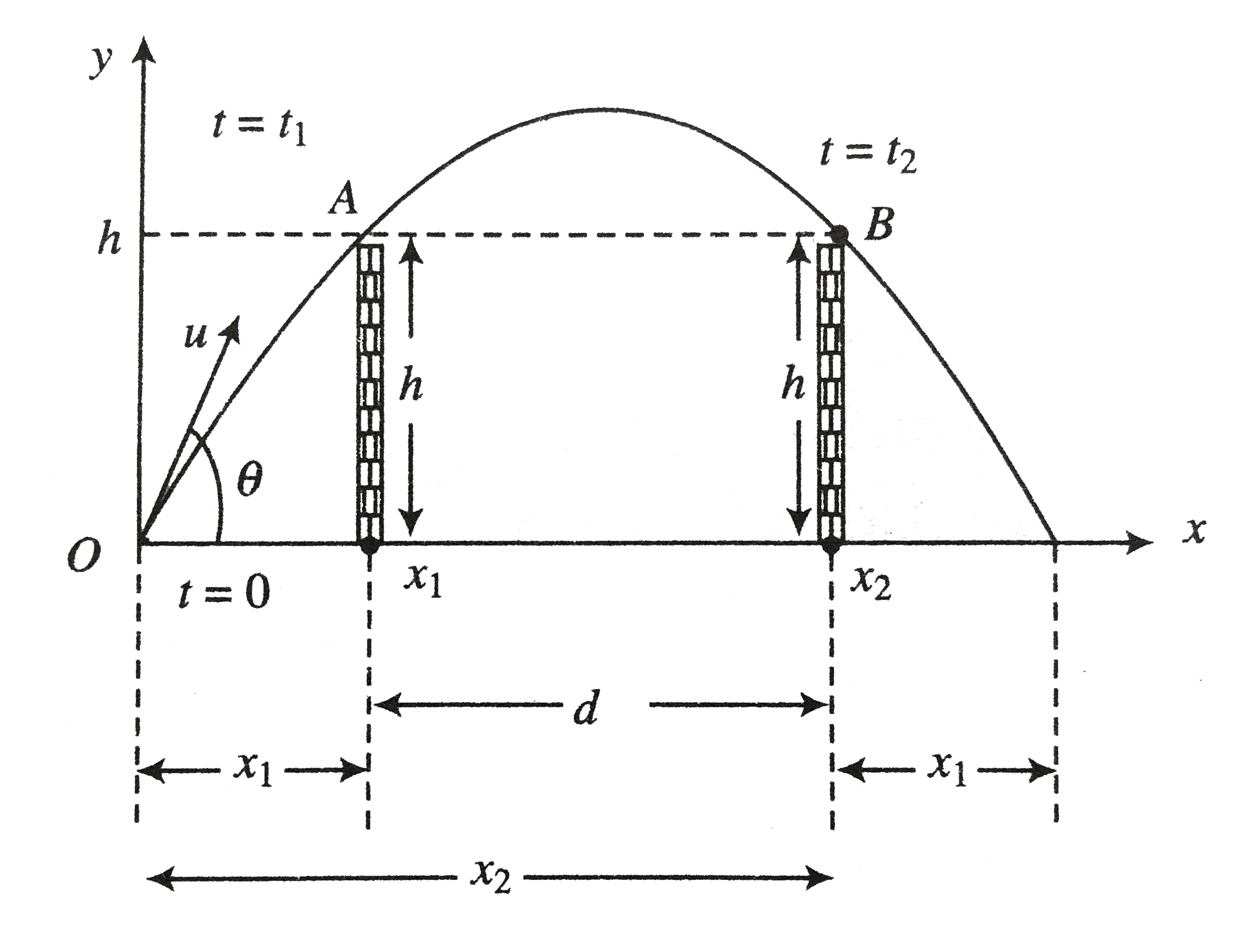
A particle is projected from the ground at $t = 0$ so that on its way it just clears two vertical walls of equal height on the ground. The particle was projected with initial velocity $u$ and at angle $θ$ with the horiozontal. If the particle passes just grazing top of the wall at time $t = t_{1} and t = t_{2}$ , then calculate.
(a) the height of the wall.
(b) the time $t_{1} and t_{2}$ in terms of height of the wall.
Write the expression for calculating the range of this projectile and separation between the walls.

Video Solution

Text Solution

Verified by Experts

$h = (u sin θ) t_{1} - \frac{1}{2} {gt}_{1}^{2}$ ….(i)
and $h = (u sin θ) t_{2} - \frac{1}{2} {gt}_{2}^{2}$ …(ii)
Comparing equation (i) with equation (ii)
$u sin θ = \frac{g (t_{1} + t_{2})}{2}$
Substituting this value in equation (i), we get
$h = g (\frac{t_{1} + t_{2}}{2}) t_{1} - \frac{1}{2} {gt}_{1}^{2} \Rightarrow h = \frac{{gt}_{1} t_{2}}{2}$
Time $(t_{1} and t_{2}) : h u sin θ t - \frac{1}{2} {gt}^{2}$
$t^{2} - \frac{2 u sin θ}{g} t + \frac{2 h}{g} = 0$
Solving for $t$ , we get
$t_{1} = \frac{u sin θ}{g} ⎡ ⎢ ⎢ ⎣ 1 + \sqrt{1 + {(\sqrt{\frac{2 g h}{u sin θ}})}^{2}} ⎤ ⎥ ⎥ ⎦$
and $t_{2} = \frac{u sin θ}{g} ⎡ ⎢ ⎣ 1 - {(\sqrt{\frac{2 g h}{u sin θ}})}^{2} ⎤ ⎥ ⎦$ .
.

A particle is projected from ground with velocity $40 \sqrt{2} m$ at $45^{\circ}$ .At time $t = 2 s$
Adisplacement of particles is $100 m$
Bvertcal component of velocity is $20 m / s$
Cvelocity makes an angle of ${tan}^{- 1} (2)$ with vertical
Dparticle is at height of $60 m$ from ground
A particle is projected at $t = 0$ with velocity u at angle $θ$ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
A $\frac{g^{2} sin 2 θ}{u^{2}}$
B $\frac{2 g^{2} sin θ}{u^{2}}$
C $\frac{g^{2} sin θ}{u^{2}}$
D $\frac{g^{2} sin 2 θ}{2 u^{2}}$
A particle is projected from ground with velocity $40 \sqrt{2} m / s$ at $45^{\circ}$ . At time $t = 2 s$
Adisplacement of particle is $100 m$
Bvertical component of velocity is $20 m / s$
Cvelocity makes an angle ${tan}^{- 1} (2)$ with vertical
Dparticle is at height of $60 m$ from ground