A particle is projected from the surface of earth with velocity equal to its escape velocity , at 45∘ with horizontal . What is the angle of its velocity with horizontal at height h = R . (Here horizontal at some point means a line parallel to tangent on earth just below that point . )
30∘
60∘
cos−1(13)
cos−1(14)
The correct Answer is:B
To solve the problem, we need to analyze the motion of a particle projected from the surface of the Earth with a velocity equal to its escape velocity at an angle of 45 degrees to the horizontal. We want to find the angle of its velocity with the horizontal when it reaches a height h=R (where R is the radius of the Earth).
Step 1: Understand the Initial Conditions
The escape velocity ve from the surface of the Earth is given by:
ve=√2GMR
where G is the universal gravitational constant and M is the mass of the Earth. The particle is projected at an angle of 45∘ with respect to the horizontal, which means its initial velocity components are:
v0x=vecos(45∘)=ve√2
v0y=vesin(45∘)=ve√2
Step 2: Analyze the Motion
As the particle moves upwards, it will experience a gravitational force acting downwards. The gravitational force decreases with height according to the formula:
g′=GM(R+h)2
At height h=R, we have:
g′=GM(R+R)2=GM4R2=g4
where g is the acceleration due to gravity at the surface of the Earth.
Step 3: Determine the Velocity Components at Height h=R
Using energy conservation, the total mechanical energy at the surface is equal to the total mechanical energy at height h=R:
12v2e=12mv2−GMmR+h
At height h=R:
12v2e=12mv2−GMm2R
Substituting v2e=2GMR:
GMR=12mv2−GMm2R
Rearranging gives:
GMR+GMm2R=12mv2
Solving for v2:
v2=2GMR+GMR=3GMR
Step 4: Find the Angle of Velocity with Horizontal
At height h=R, the vertical component of velocity will be affected by gravity. The vertical component of velocity vy can be found using:
vy=v0y−g′t
where g′=g4 and t is the time taken to reach height R.
The horizontal component vx remains constant:
vx=v0x=ve√2
The angle θ with respect to the horizontal can be calculated using:
tan(θ)=vyvx
Step 5: Calculate the Final Angle
Using the values we derived:
tan(θ)=vyvx=ve√2−g4tve√2
To find t, we can use the kinematic equations or energy conservation principles, but since we are looking for the angle, we can directly relate vy and vx to find θ.
Finally, substituting the values and simplifying will yield the angle θ.
Conclusion
The angle of the velocity with the horizontal at height h=R can be determined through the above calculations.
The escape velocity ve from the surface of the Earth is given by:
ve=√2GMR
where G is the universal gravitational constant and M is the mass of the Earth. The particle is projected at an angle of 45∘ with respect to the horizontal, which means its initial velocity components are:
v0x=vecos(45∘)=ve√2
v0y=vesin(45∘)=ve√2
As the particle moves upwards, it will experience a gravitational force acting downwards. The gravitational force decreases with height according to the formula:
g′=GM(R+h)2
At height h=R, we have:
g′=GM(R+R)2=GM4R2=g4
where g is the acceleration due to gravity at the surface of the Earth.
Using energy conservation, the total mechanical energy at the surface is equal to the total mechanical energy at height h=R:
12v2e=12mv2−GMmR+h
At height h=R:
12v2e=12mv2−GMm2R
Substituting v2e=2GMR:
GMR=12mv2−GMm2R
Rearranging gives:
GMR+GMm2R=12mv2
Solving for v2:
v2=2GMR+GMR=3GMR
At height h=R, the vertical component of velocity will be affected by gravity. The vertical component of velocity vy can be found using:
vy=v0y−g′t
where g′=g4 and t is the time taken to reach height R.
vx=v0x=ve√2
tan(θ)=vyvx
Using the values we derived:
tan(θ)=vyvx=ve√2−g4tve√2
The angle of the velocity with the horizontal at height h=R can be determined through the above calculations.
Topper's Solved these Questions
Similar Questions
A body is projected at angle of 45∘ to the horizontal . What is its velocity at the highest point ?
View SolutionA body is projected from the surface of the earth with thrice the escape velocity (Ve) from the surface of the earth. What will be its velocity, when it will escape the gravitational pull?
View Solution
Knowledge Check
- Question 1 - Select One
An object is projected from the earth's surface with escape velocity at 30∘ with horizontal. What is the angle made by the velocity with horizontal when the object reaches a height 2R from the earth's surface ? R is the radius of the earth. Horizontal can be considered as a line parallel to the tangent at the earth's surface just below the object .
A30∘B45∘C60∘D15∘ - Question 2 - Select One
A particle is thrown with escape velocity ve from the surface of earth. Calculate its velocity at height 3 R :-
A≅9.25 km/sB≅5.6 km/sC≅11.2 km/sD≅4.3 km/s - Question 3 - Select One
A particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
AVelocity of particle at Q is vsinθBVelocity of particle at Q is vcotθCTime of flight from P to Q is (v/g)cosecθDTime of flight from P to Q is (v/g)secθ
A body is projected vertically up from surface of the earth with a velocity half of escape velocity. The ratio of its maximum height of ascent and radius of earth is
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View SolutionA piece of marble is projected from earth's surface with velocity of 19.6√2ms−1 at 45∘. 2 s later its velocity makes an angle α with horizontal, where α is
View SolutionA particle is projected from a point A with velocity u√2 at an angle of 45∘ with horizontal as shown in the figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is
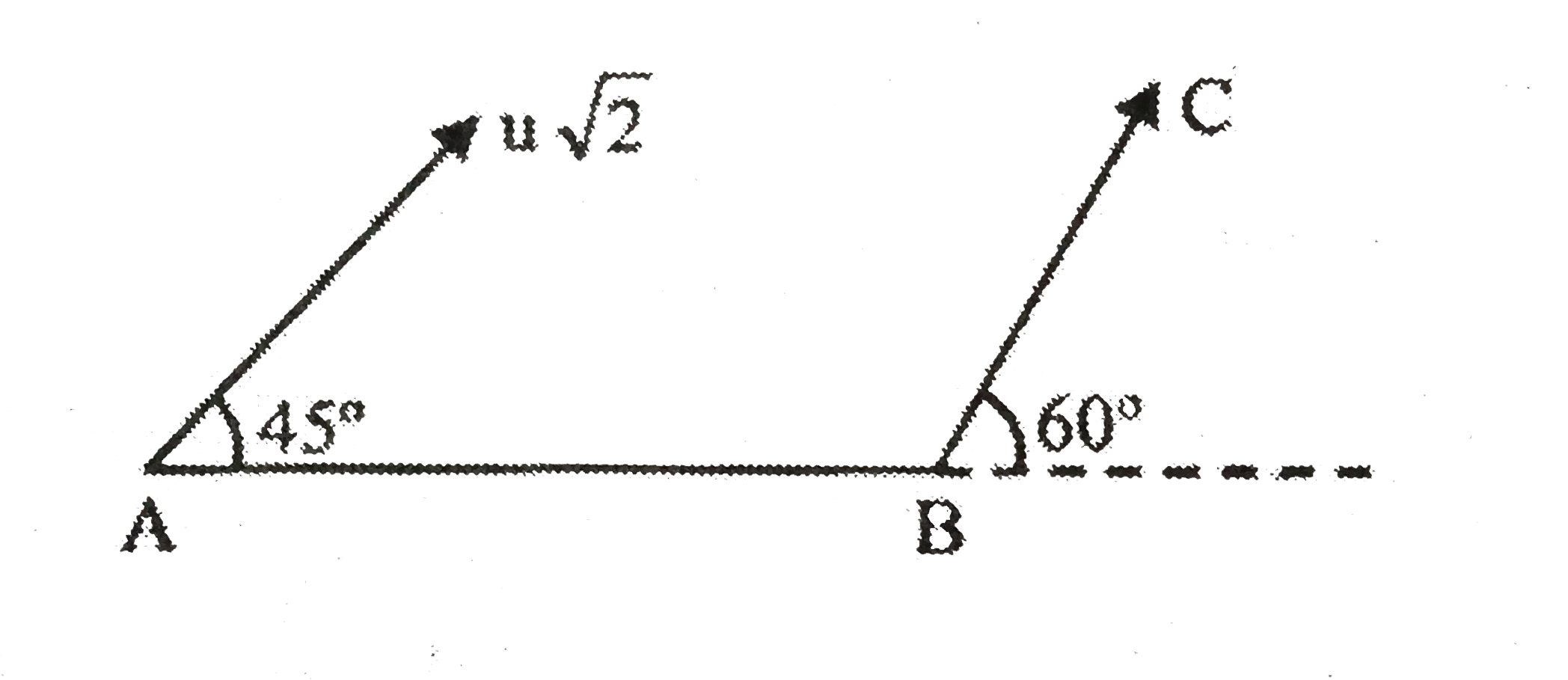 View Solution
View SolutionA particle is projected from a point A with velocity √2u an angle of 45∘ with horizontal as shown in figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is
 View Solution
View Solution

