A particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?
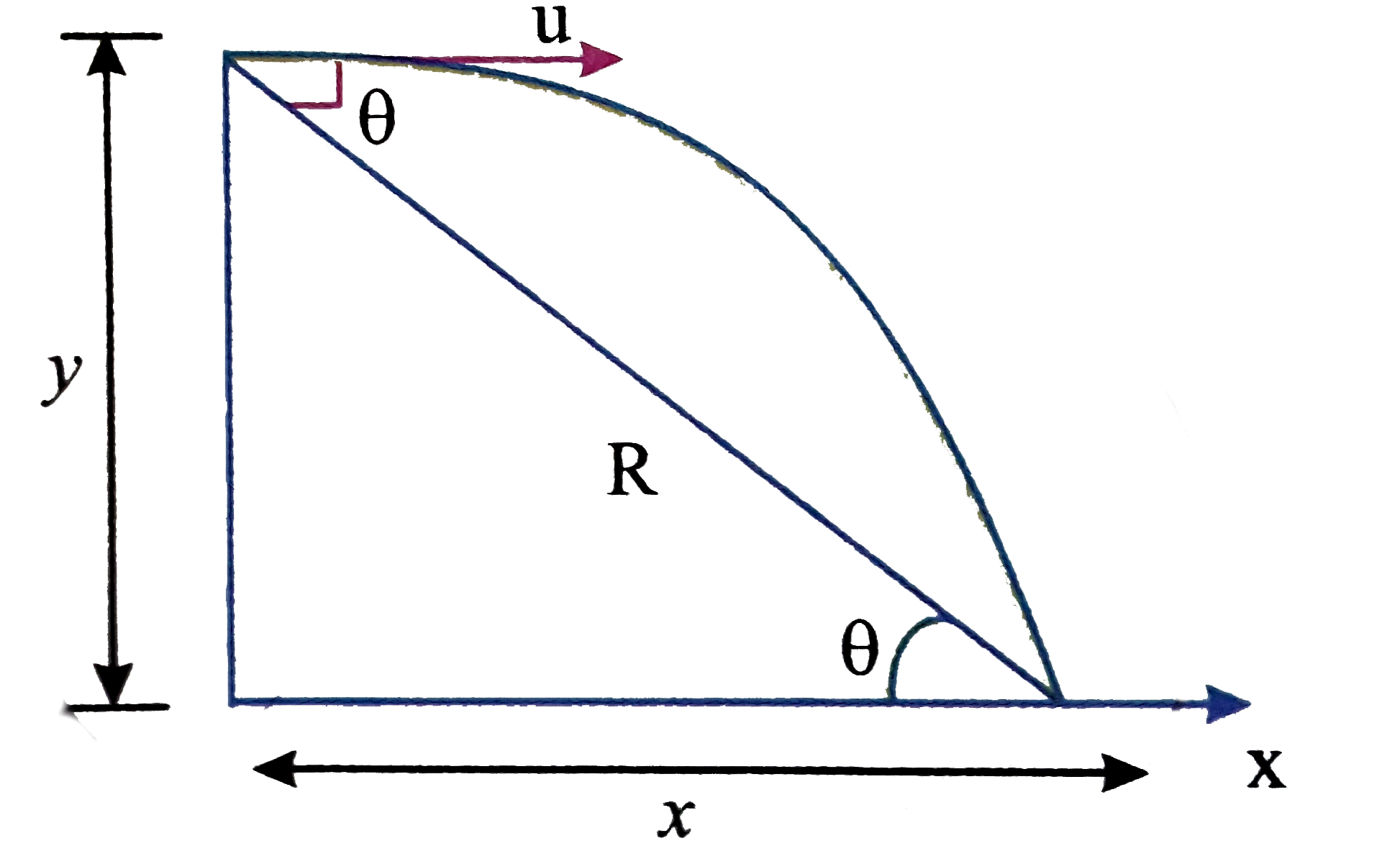
Take X,Y-axis as shown in ure Suppose that the particle strikes the plane at a point P with coordiN/Ates (x,y). Consider the motion between A and P.
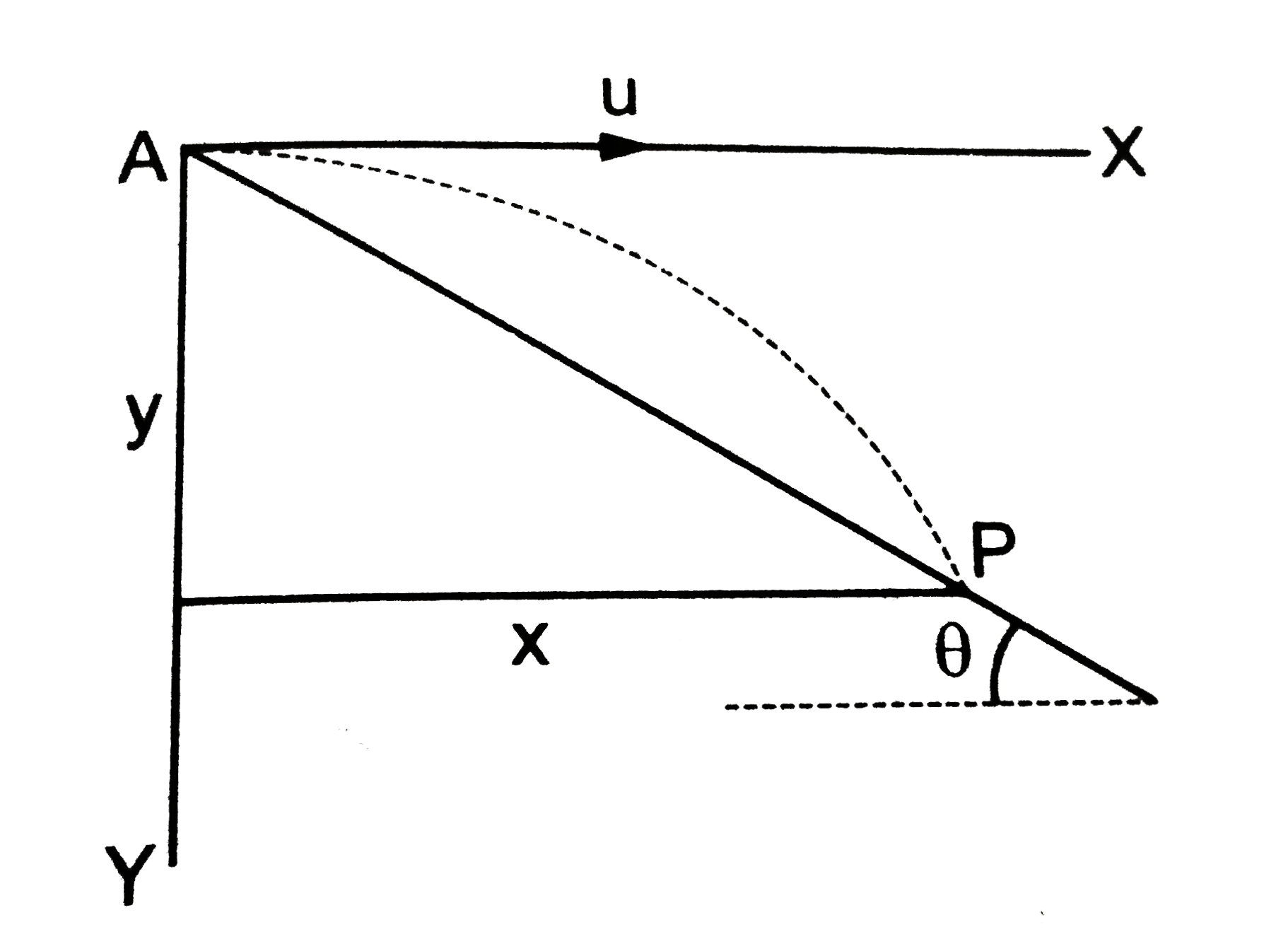
Motion in x- direction
Initialvelocity=u
Ae≤ration=g
y=12>2
ElimiN/Ating t from i. and ii
y=12gx2u2
Also y=xtanθ
Thus,(gx^2)/(2u^2)=x tan theta giv∈gx=0, or, 2u2tanθg,<br>theny= x tantheta= (2u^2 tan^2 theta)/g<br>ThedistanceAP=l=sqrt(x^2+y^2)<br>=(2u^2)/g tan theta sqrt (1+tan^2theta)<br>=(2u^2)/g tantheta sec theta.A<erNAtively:Taketheaxesasshown∈ure.consrthemotionbetweenAandP.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C03_S01_024_S02.pngwh=80%mx-autosty≤=background:white;><br>MotionalongtheX−aξs:<br>Intialvelocity=u cos theta<br>Ae≤ration=g sin theta<br>Displacement =AP.<br>Thus,AP=(u cos theta)t+1/2(g sin theta)t^2<br>MotionalongtheY−aξs<br>Initial velocity =-u sin theta<br>acceleration =g cos theta<br>Displacement =0<br>Thus, 0=- uy sin theta +1/2 gt^2 cos theta<br>or, t=0,2usinθg(cosθ)
clearly the point P corresponds to t=2usinθgcosθ
Putting this value of t in i.
AP=(ucosθ)(2usinθgcosθ)+gsinθ2(2usinθgcosθ)2
2u2sinθg+2u2sinθtan2θg
=2u2gsinθsec2θ=2u2gtanθsecθ.
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -1
13 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -2
9 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
Similar Questions
A ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View SolutionA particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA particle is projected at an angle θ with an initial speed u.
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View Solution
A particle is projected from surface of the inclined plane with speed u and at an angle θ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionA particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
View Solution
