A particle is projected up a rough inclined plane of inclination θ and friction coefficient μ. If the time of ascent is half of the time of descent, the friction coefficient μ is equal to
34tanθ
35tanθ
45tanθ
12tanθ
The correct Answer is:B
To solve the problem of a particle projected up a rough inclined plane with inclination angle θ and friction coefficient μ, we need to analyze the motion of the particle during its ascent and descent.
1. Identify Forces Acting on the Particle:
- When the particle is moving up, the forces acting on it are:
- Gravitational force mg acting downwards.
- Frictional force f acting down the incline (opposite to the direction of motion).
- The gravitational force can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
2. Determine the Acceleration During Ascent:
- The net force acting on the particle while it ascends is given by:
Fnet=−mgsinθ−f
- The frictional force f can be expressed as f=μN, where N=mgcosθ (the normal force). Thus, f=μmgcosθ.
- The equation for net force becomes:
Fnet=−mgsinθ−μmgcosθ
- Using Newton's second law, F=ma:
ma=−mgsinθ−μmgcosθ
- Dividing by m gives the acceleration a1 during ascent:
a1=−gsinθ−μgcosθ
3. Determine the Acceleration During Descent:
- When the particle descends, the forces acting on it are:
- Gravitational force mg acting downwards.
- Frictional force f acting up the incline.
- The net force during descent is:
Fnet=mgsinθ−f
- The frictional force remains f=μmgcosθ.
- The equation for net force becomes:
Fnet=mgsinθ−μmgcosθ
- Using Newton's second law:
ma=mgsinθ−μmgcosθ
- Dividing by m gives the acceleration a2 during descent:
a2=gsinθ−μgcosθ
4. Relate Time of Ascent and Descent:
- Given that the time of ascent T1 is half the time of descent T2:
T1=12T2
- The distance s covered during ascent and descent is the same, so we can use the equations of motion:
- For ascent:
s=uT1−12a1T21
- For descent:
s=12a2T22
5. Set Up the Equation:
- Since T1=12T2, substitute T1 in the ascent equation:
s=u(12T2)−12a1(12T2)2
- Simplifying gives:
s=u2T2−18a1T22
- For descent:
s=12a2T22
6. Equate the Two Distances:
- Set the two expressions for s equal:
u2T2−18a1T22=12a2T22
- Rearranging gives:
uT2−14a1T22=a2T22
7. Substitute for Accelerations:
- Substitute a1 and a2 into the equation:
uT2−14(−gsinθ−μgcosθ)T22=(gsinθ−μgcosθ)T22
8. Solve for μ:
- Rearranging and simplifying leads to:
5μgcosθ=3gsinθ
- Dividing by g gives:
5μcosθ=3sinθ
- Thus, the friction coefficient μ is:
μ=3sinθ5cosθ=35tanθ
Final Answer:
The friction coefficient μ is given by:
μ=35tanθ
- When the particle is moving up, the forces acting on it are:
- Gravitational force mg acting downwards.
- Frictional force f acting down the incline (opposite to the direction of motion).
- The gravitational force can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
- The net force acting on the particle while it ascends is given by:
Fnet=−mgsinθ−f
- The frictional force f can be expressed as f=μN, where N=mgcosθ (the normal force). Thus, f=μmgcosθ.
- The equation for net force becomes:
Fnet=−mgsinθ−μmgcosθ
- Using Newton's second law, F=ma:
ma=−mgsinθ−μmgcosθ
- Dividing by m gives the acceleration a1 during ascent:
a1=−gsinθ−μgcosθ
- When the particle descends, the forces acting on it are:
- Gravitational force mg acting downwards.
- Frictional force f acting up the incline.
- The net force during descent is:
Fnet=mgsinθ−f
- The frictional force remains f=μmgcosθ.
- The equation for net force becomes:
Fnet=mgsinθ−μmgcosθ
- Using Newton's second law:
ma=mgsinθ−μmgcosθ
- Dividing by m gives the acceleration a2 during descent:
a2=gsinθ−μgcosθ
- Given that the time of ascent T1 is half the time of descent T2:
T1=12T2
- The distance s covered during ascent and descent is the same, so we can use the equations of motion:
- For ascent:
s=uT1−12a1T21
- For descent:
s=12a2T22
- Since T1=12T2, substitute T1 in the ascent equation:
s=u(12T2)−12a1(12T2)2
- Simplifying gives:
s=u2T2−18a1T22
- For descent:
s=12a2T22
- Set the two expressions for s equal:
u2T2−18a1T22=12a2T22
- Rearranging gives:
uT2−14a1T22=a2T22
- Substitute a1 and a2 into the equation:
uT2−14(−gsinθ−μgcosθ)T22=(gsinθ−μgcosθ)T22
- Rearranging and simplifying leads to:
5μgcosθ=3gsinθ
- Dividing by g gives:
5μcosθ=3sinθ
- Thus, the friction coefficient μ is:
μ=3sinθ5cosθ=35tanθ
The friction coefficient μ is given by:
μ=35tanθ
Topper's Solved these Questions
Similar Questions
(a) A block slides down an incline of angle 45∘ with an acceleration g2√2. Find the friction coefficient.
(b) A block slides down at 45∘ inclined plane in twice the time it takes to slide down a smooth 45∘ incline. What is friction co-efficient between the block and the incline?
( c) A block slides down on a rough inclined plane of inclination 30∘ with constant velocity. If this block is projected up the plane with a velocity of 10m/s, then at what distance along the inclined plane , the block will come to rest?
(d) A body is launched up on a rough inclined plane of inclination θ. If time of ascent is half of time of descent, find the friction coefficient.View SolutionA block is pushed up a rough inclined plane of 45∘ .If the time of descent is three times the time of ascent,the coefficient of friction is ?
View Solution
Knowledge Check
- Question 1 - Select One
A body is projected up along a rough inclined plane of inclination 45∘ . The coefficient of friction is 0.5. Then the retardation of the block is
Ag2√2Bg2C3g2√2Dg√2 - Question 2 - Select One
A particle is projected directly along a rough plane of inclination θ with velocity u. If after coming to the rest the particle returns to the starting point with velocity v, the coefficient of friction between the partice and the plane is
Au2v2tanθBu2−v2u2+v2tanθCv2u2tanθDu2+v2u2−v2tanθ - Question 3 - Select One or More
A block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
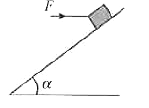 ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
A body of mass M is placed on a rough inclined plane of inclination θ and coefficient of friction μk. A force of (mgsinθ+μkmgcosθ) is applied in the upward direction, the acceleration of the body is
View SolutionA body of mass M is placed on a rough inclined plane of inclination θ and coefficient of friction μk A force of (mgsinθ+μkmgcosθ) is applied in the upward direction the acceleration of the body is .
View SolutionA block is kept on an inclined plane of inclination θ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friction is μ)
View SolutionA uniform solid sphere of mass m and radius 'R' is imparted an initial velocity v0 and angular ω0=2v0R and then placed on a rough inclined plane of inclination 'theta' and coefficient of friction μ=2tanθ as shown. The time after which the sphere will start rolling without slipping is
 View Solution
View SolutionA block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
View Solution

