A particle is released from rest from a tower of height 3h. The ratio of time intervals for fall of equal height h i.e. t1:t2:t3 is :
5:3:1
3:2:1
9:4:1
1:(√2−1):(√3:√2)
The correct Answer is:D
To solve the problem of finding the ratio of time intervals t1:t2:t3 for a particle falling from a height of 3h in equal segments of height h, we can follow these steps:
Step 1: Define the heights and time intervals
The particle is released from a height of 3h. We can divide this height into three equal parts:
- From point A (height = 3h) to point B (height = 2h): height = h
- From point B (height = 2h) to point C (height = h): height = h
- From point C (height = h) to point D (height = 0): height = h
Let:
- t1 = time taken to fall from A to B
- t2 = time taken to fall from B to C
- t3 = time taken to fall from C to D
Step 2: Calculate t1
Using the second equation of motion for the first segment (A to B):
s=ut+12gt2
Here, s=h, u=0 (initial velocity), and g is the acceleration due to gravity. Thus:
h=0+12gt21
Rearranging gives:
t21=2hg
Taking the square root:
t1=√2hg
Step 3: Calculate t2
For the second segment (B to C), the particle has already fallen h from A to B, so it starts from rest at height 2h. The total distance fallen from A to C is 2h:
2h=0+12gt2AC
Rearranging gives:
t2AC=4hg
Taking the square root:
tAC=√4hg=2√hg
Now, to find t2:
t2=tAC−t1=2√hg−√2hg=√hg(2−√2)
Step 4: Calculate t3
For the third segment (C to D), the total distance fallen from A to D is 3h:
3h=0+12gt2AD
Rearranging gives:
t2AD=6hg
Taking the square root:
tAD=√6hg
Now, to find t3:
t3=tAD−tAC=√6hg−2√hg=√hg(√6−2)
Step 5: Find the ratio t1:t2:t3
Now we have:
- t1=√2hg
- t2=√hg(2−√2)
- t3=√hg(√6−2)
To find the ratio, we can express all terms in terms of √hg:
t1:t2:t3=√2:(2−√2):(√6−2)
Final Ratio
Thus, the final ratio of time intervals is:
t1:t2:t3=√2:(2−√2):(√6−2)
The particle is released from a height of 3h. We can divide this height into three equal parts:
- From point A (height = 3h) to point B (height = 2h): height = h
- From point B (height = 2h) to point C (height = h): height = h
- From point C (height = h) to point D (height = 0): height = h
- t1 = time taken to fall from A to B
- t2 = time taken to fall from B to C
- t3 = time taken to fall from C to D
Using the second equation of motion for the first segment (A to B):
s=ut+12gt2
Here, s=h, u=0 (initial velocity), and g is the acceleration due to gravity. Thus:
h=0+12gt21
Rearranging gives:
t21=2hg
Taking the square root:
t1=√2hg
For the second segment (B to C), the particle has already fallen h from A to B, so it starts from rest at height 2h. The total distance fallen from A to C is 2h:
2h=0+12gt2AC
Rearranging gives:
t2AC=4hg
Taking the square root:
tAC=√4hg=2√hg
Now, to find t2:
t2=tAC−t1=2√hg−√2hg=√hg(2−√2)
For the third segment (C to D), the total distance fallen from A to D is 3h:
3h=0+12gt2AD
Rearranging gives:
t2AD=6hg
Taking the square root:
tAD=√6hg
Now, to find t3:
t3=tAD−tAC=√6hg−2√hg=√hg(√6−2)
Now we have:
- t1=√2hg
- t2=√hg(2−√2)
- t3=√hg(√6−2)
t1:t2:t3=√2:(2−√2):(√6−2)
Thus, the final ratio of time intervals is:
t1:t2:t3=√2:(2−√2):(√6−2)
Topper's Solved these Questions
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:MCQ_TYPE
Explore 27 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:COMPREHENSION_TYPE
Explore 19 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Medical entrances gallery
Explore 39 Videos
Similar Questions
A particle is released from rest from a tower of height 3h. The ratio of times to fall equal heights 'h' i.e. t1:t2:t3 is (√3 =1.17 & √2 = 1.4)
View SolutionLet A, B and C be points in a vertical line at height h, 4h5andh5 and from the ground. A particle released from rest from the point A reaches the ground in time T. The time taken by the particle to go from B to C is TBC . Then T(TBC)2=
View Solution
Knowledge Check
A body is released form the top of a tower of height h meters. It takes t seconds to reach the ground. Where is the ball at the time t/2 sec ?
Aat h/2 meter from the groundBat h/4 meter from the groundCdepends upon the mass and volume of the ballDat 3h/4 meter from the ground.
A particle is projected from the ground at t=0 so that on its way it just clears two vertical walls of equal height on the ground. The particle was projected with initial velocity u and at angle θ with the horiozontal. If the particle passes just grazing top of the wall at time t=t1andt=t2, then calculate.
(a) the height of the wall.
(b) the time t1andt2 in terms of height of the wall.
Write the expression for calculating the range of this projectile and separation between the walls.
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA body is released from the top of a tower of height h and takes 'T' sec to reach the ground. The position of the body at T/2 sec is
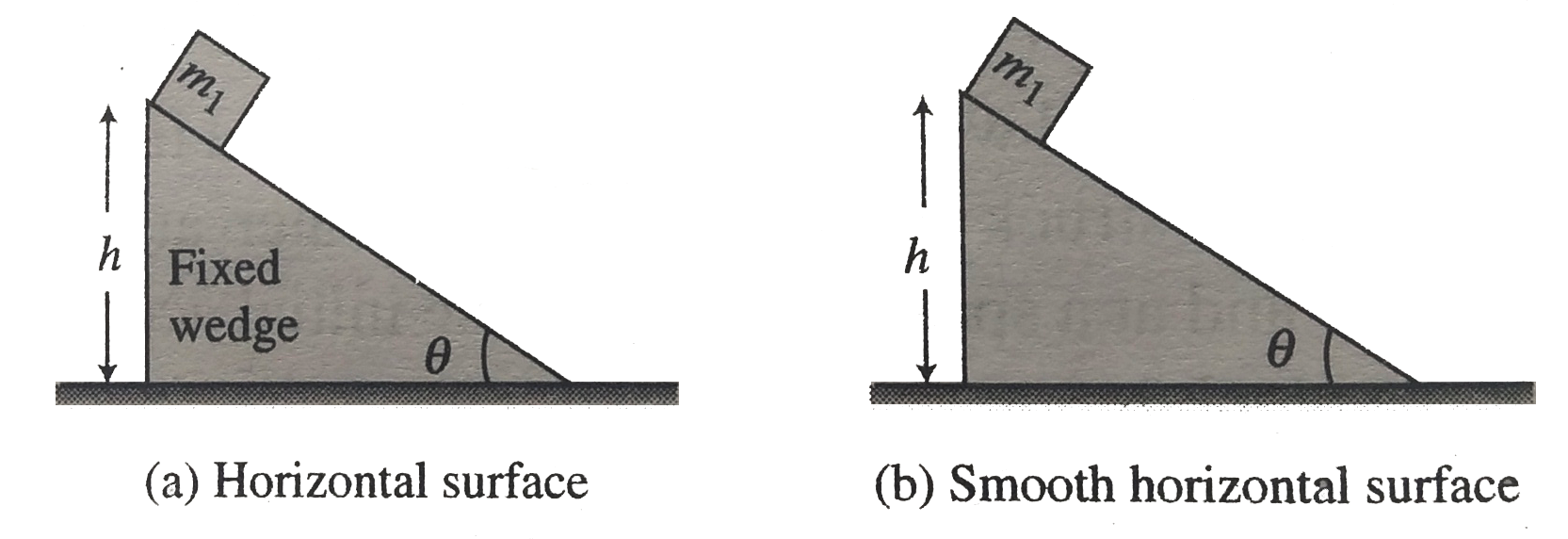
View SolutionA block of mass m1 lies on the top of fixed wedge as shown in fig. and another block of mass m2 lies on top of wedge which is free to move as shown in fig. At time t=0 both the blocks are released from rest from a vertical height h above the respective horizontal surface on which the wedge is placed as shown. There is no friction between block and wedge in both the figures. Let T1 and T2 be the time taken by the blocks respectively to just reach the horizontal surface. then
View Solution