Two particles P and Q simultaneously start moving from point A with velocities 15m/s and 20m/s respectively. The two particles move with acceleration equal in magnitude but opposite in direction. When P overtakes Q at point B then its velocity is 30m/s, the velocity of Q at point B will be
The correct Answer is:5
To find the velocity of particle Q at point B when particle P overtakes it, we can follow these steps:
1. Identify the initial conditions:
- Particle P starts with an initial velocity uP=15m/s.
- Particle Q starts with an initial velocity uQ=20m/s.
- Both particles have equal magnitudes of acceleration but in opposite directions. Let the acceleration of P be a and the acceleration of Q be −a.
2. Use the final velocity of particle P:
- When particle P overtakes particle Q at point B, its final velocity is given as vP=30m/s.
3. Apply the equation of motion for particle P:
- We can use the equation of motion:
v=u+at
- For particle P:
30=15+atP
- Rearranging gives:
atP=30−15=15(1)
4. Apply the equation of motion for particle Q:
- For particle Q, we use the same equation of motion:
v=u+at
- Since the acceleration is in the opposite direction, we have:
vQ=20−atQ
- We need to find the time tQ when P overtakes Q. Since both particles start at the same time and P overtakes Q, we can assume tP=tQ=t.
5. Substituting t into the equations:
- From equation (1), we have at=15. Therefore, we can express a as:
a=15t(2)
- Substitute a from (2) into the equation for Q:
vQ=20−(15t)t
- Simplifying gives:
vQ=20−15=5m/s
Final Answer:
The velocity of particle Q at point B is 5m/s.
- Particle P starts with an initial velocity uP=15m/s.
- Particle Q starts with an initial velocity uQ=20m/s.
- Both particles have equal magnitudes of acceleration but in opposite directions. Let the acceleration of P be a and the acceleration of Q be −a.
- When particle P overtakes particle Q at point B, its final velocity is given as vP=30m/s.
- We can use the equation of motion:
v=u+at
- For particle P:
30=15+atP
- Rearranging gives:
atP=30−15=15(1)
- For particle Q, we use the same equation of motion:
v=u+at
- Since the acceleration is in the opposite direction, we have:
vQ=20−atQ
- We need to find the time tQ when P overtakes Q. Since both particles start at the same time and P overtakes Q, we can assume tP=tQ=t.
- From equation (1), we have at=15. Therefore, we can express a as:
a=15t(2)
- Substitute a from (2) into the equation for Q:
vQ=20−(15t)t
- Simplifying gives:
vQ=20−15=5m/s
The velocity of particle Q at point B is 5m/s.
Topper's Solved these Questions
Similar Questions
Two elastic bodies P and Q having equal mases are moving along the same line with velocities of 16 m/s and 10 m/s respectively. Their velocities after the elastic collision will be in m/s :
View SolutionTwo perfectly elastic particles A and B of equal masses travelling along a line joining them with velocities 15m/s and 10m/s respectively collide. Their velocities after the elastic collision will be (in m/s) respectively
View SolutionTwo perfectly elastic particles A and B of equal masses travelling along a line joining them with velocities 15m/s and 10m/s respectively collide. Their velocities after the elastic collision will be (in m/s) respectively
View SolutionTwo cars A and B cross a point P with velocities 10m/s and 15m/s. After that they move with different uniform accelerations and the car A overtakes B with a speed of 25ms−1. What is velocity of B at that instant?
View SolutionThe velocity of a projectile at the initial point A is (2ˆi+3ˆj)m/s. Its velocity (in m/s) at point B is

View SolutionTwo particles 1 and 2 are thrown in the directions shown in figure simultaneously with velocities 5m/sand20m/s. Initially, particle 1 is at height 20 m from the ground. Taking upwards as the positive direction, find

(a) acceleration of 1 with respect to 2
(b) initial velocity of with respect to 1
(c) velocity of 1 with respect to 2 after time t=12s
(d) time when the particles will collide.
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
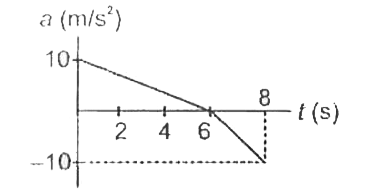
View SolutionA body travelling with uniform acceleration crosses two point A and B with velocities 20ms−1 and 30ms−1 respectively. The speed of the body at the mid-point of A and B is.
View SolutionTwo smooth spheres A and B of masses 4kg and 8kg move with velocities 9m/s and 3m/s in opposite directions. If A rebounds on its path with velocity 1m/s, then
View SolutionThe velocity of a particle moving with constant acceleration at an instant t0 is 10m/s After 5 seconds of that instant the velocity of the particle is 20m/s. The velocity at 3 second before t0 is:-
View Solution
