A particle is released from the top of a smooth hemisphere.find the angle rotated by the radius through the particle, when it loses contract with the hemisphere. Also sketch variation of normal contact force with cosθ, where θ is an angle rotated by the radius through the particle.
h=R−Rcosθ
v2=u2+2gh=0+2gR(1−cosθ)
mgcosθ−N=mv2R=mR2gR(1−cosθ)
N=3mgcosθ−2mg
when the particle loses contact, normal contact force vanishes.
0=3mgcosθ−2mg
cosθ=23⇒θ=cos−1(23)
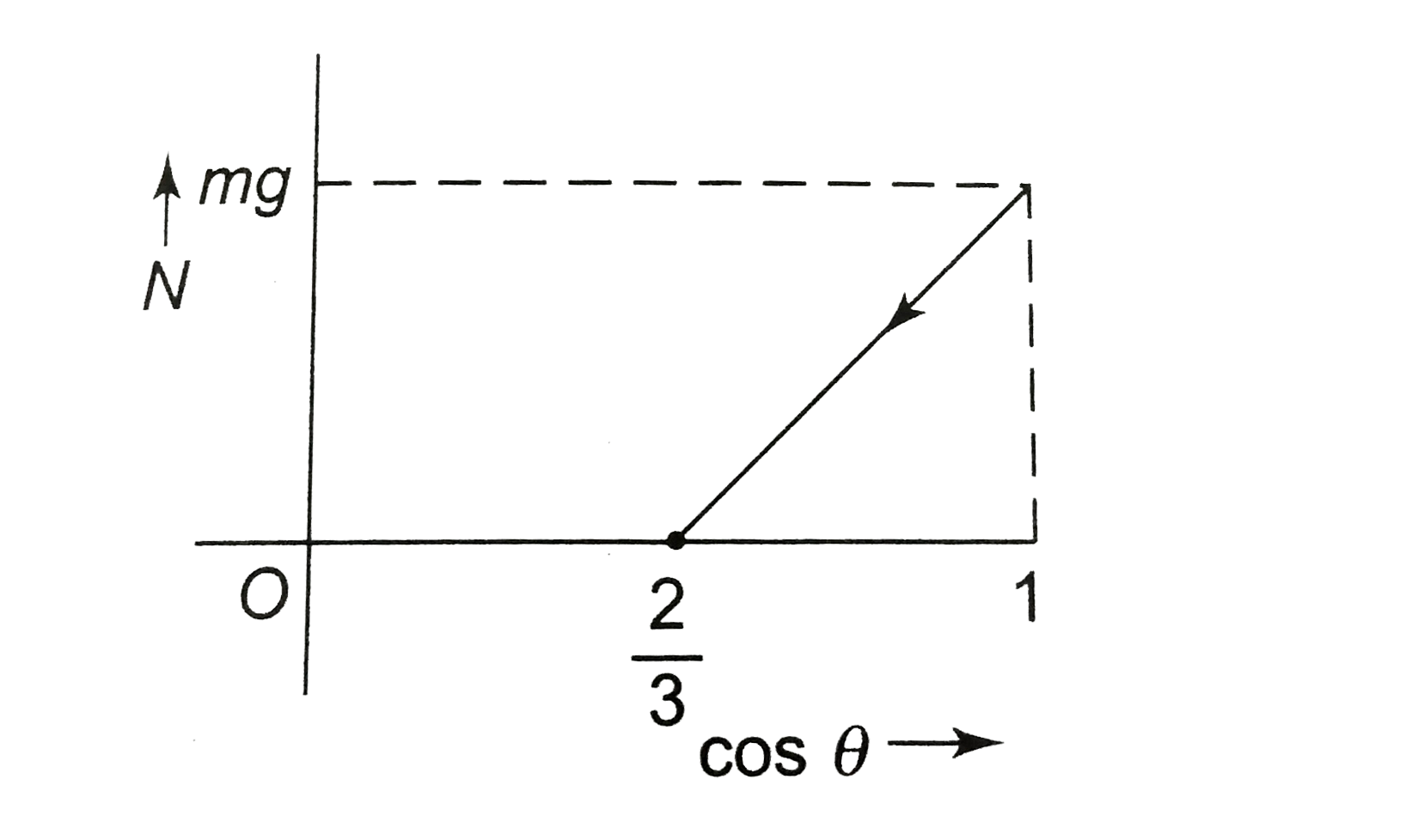
Nv/scosθ
N=3mgcosθ−2mg
θ=0⇒cosθ=1⇒N=mg
cosθ=23⇒N=0
shape: y=3mgx−2mg (straight line)
y=Mx+C(M=3mg, slope is positive, C=−2mg, intercept is negative)

Topper's Solved these Questions
Similar Questions
A particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View Solution
Knowledge Check
A particle is released from the top of the smooth hemisphere R as shown.
the normal contact between the particle and the hemisphere in position θ is
 Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)A partcle rests on the top of a hemisphere of radiu R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down it-
A√gRB√2gRC√3gRD√5gRA partcle rests on the top of a hemisphere of radius R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down :
A√gRB√2gRC√3gRD√5gR
A block of mass as shown is released from rest from top of a fixed smooth hemisphere. Find angle made by this particle with vertical at the instant when it looses contact with hemisphere.
View SolutionA particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.

View SolutionA particle of mass m is released on a fixed. Smooth sphere of radius R at a position, where the radius through the particle makes an angle of α with the verticle. What is the angle made by radius through the particle when the particle loses contact with sphere? (cosα=3/4)
View SolutionA particle of mass m is released in a smooth hemispherical bowl from shown position A. Find work done by gravity as it reaches the lowest point B.
View SolutionA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
View Solution
