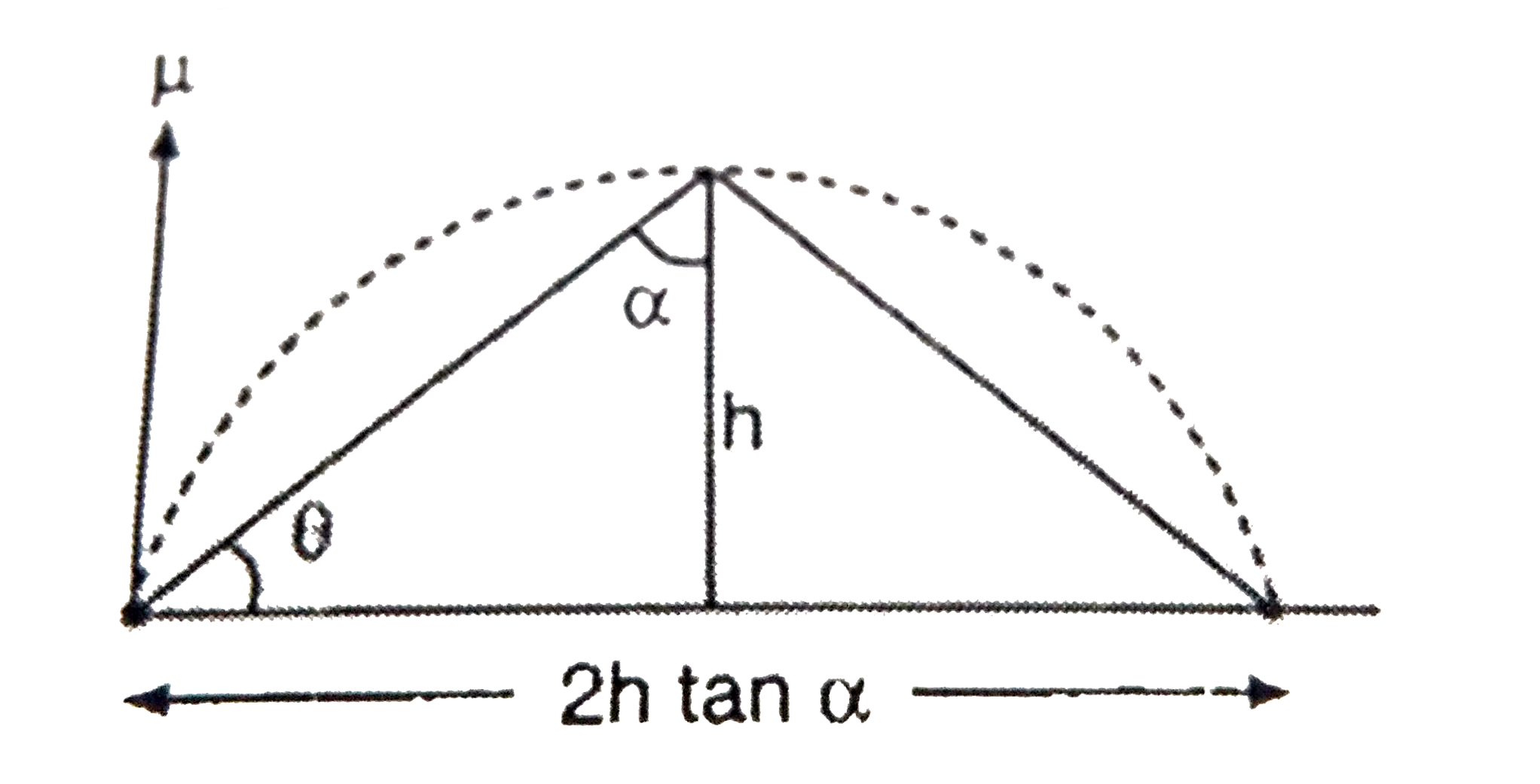
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
The correct Answer is:A
To prove that tanθ=tanα+tanβ, we will follow these steps:
Step 1: Define the Triangle and Variables
Let triangle ABC have base AB with angles α at point A and β at point B. The height from point C to base AB is y. The horizontal distance from point A to the vertex C is x, and the distance from vertex C to point B is r−x, where r is the total length of the base AB.
Step 2: Express Tangents in Terms of Height and Distances
Using the definition of tangent in right triangles:
- For angle α:
tanα=yx
- For angle β:
tanβ=yr−x
Step 3: Add the Tangents
Now, we can add the two expressions for tanα and tanβ:
tanα+tanβ=yx+yr−x
Step 4: Find a Common Denominator
To combine the fractions, we find a common denominator:
tanα+tanβ=y(r−x)+yxx(r−x)=yrx(r−x)
Step 5: Use the Equation of Trajectory
The equation of the projectile's trajectory can be expressed as:
y=xtanθ(1−xr)
From this, we can rearrange to find:
y=xtanθ−x2tanθr
Step 6: Substitute for y
Now, we can express y in terms of tanθ:
y=xtanθrr−x
Step 7: Equate the Two Expressions for y
Now we have two expressions for y:
1. From the tangent addition:
y=yrx(r−x)
2. From the trajectory equation:
y=xtanθrr−x
Equating these gives:
yrx(r−x)=xtanθrr−x
Step 8: Simplify and Conclude
By simplifying, we find:
tanθ=tanα+tanβ
Thus, we have proved that:
tanθ=tanα+tanβ
Let triangle ABC have base AB with angles α at point A and β at point B. The height from point C to base AB is y. The horizontal distance from point A to the vertex C is x, and the distance from vertex C to point B is r−x, where r is the total length of the base AB.
Using the definition of tangent in right triangles:
- For angle α:
tanα=yx
- For angle β:
tanβ=yr−x
Now, we can add the two expressions for tanα and tanβ:
tanα+tanβ=yx+yr−x
To combine the fractions, we find a common denominator:
tanα+tanβ=y(r−x)+yxx(r−x)=yrx(r−x)
The equation of the projectile's trajectory can be expressed as:
y=xtanθ(1−xr)
From this, we can rearrange to find:
y=xtanθ−x2tanθr
Now, we can express y in terms of tanθ:
y=xtanθrr−x
Now we have two expressions for y:
1. From the tangent addition:
y=yrx(r−x)
2. From the trajectory equation:
y=xtanθrr−x
yrx(r−x)=xtanθrr−x
By simplifying, we find:
tanθ=tanα+tanβ
tanθ=tanα+tanβ
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Exercise 7.1
5 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Exercise 7.2
10 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 5
3 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A particle is projected over a traingle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If α and β be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ.
View SolutionA particle is projected over a triangle from one extremity of its horizontal base. Grazing over the vertex, it falls on the other extremity of the base. If aandb are the base angles of the triangle and θ the angle of projection, prove that tanθ=tan∝+tanβ.
View Solution
Knowledge Check
A particle is thrown over a triangle from one end of horizontal base and grazing over the vertex falls on the other end of the base. If α,β are the base angles and θ the angle of projection, then
Atanθ=tanα−tanβBtanθ=tanβ−tanαCtanθ=tanα+tanβDNone of theseA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If 30∘and60∘ be the base angles and θ the angle of projection then tanθ is
A2√3B4√3C13D3If a cos2θ+bsin2θ=c has αandβ as its solution, then the value of tanα+tanβ is
Ac+a2bB2bc+aCc−a2bDbc+a
A particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionIf αandβ are roots of the equatioin acosθ+bsinθ=c, then find the value of tan(α+β).
View SolutionA projectile is fired from the base of cone shaped hill. The projectle grazes the vertex and strikes the hill again at the base. If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then tanθtanα is:
View SolutionIf tanβ=cosθtanα, then tan2θ2=
View SolutionIf αandβ are the solutions of the equation atanθ+bsecθ=c, then show that tan(α+β)=2aca2−c2
View Solution
