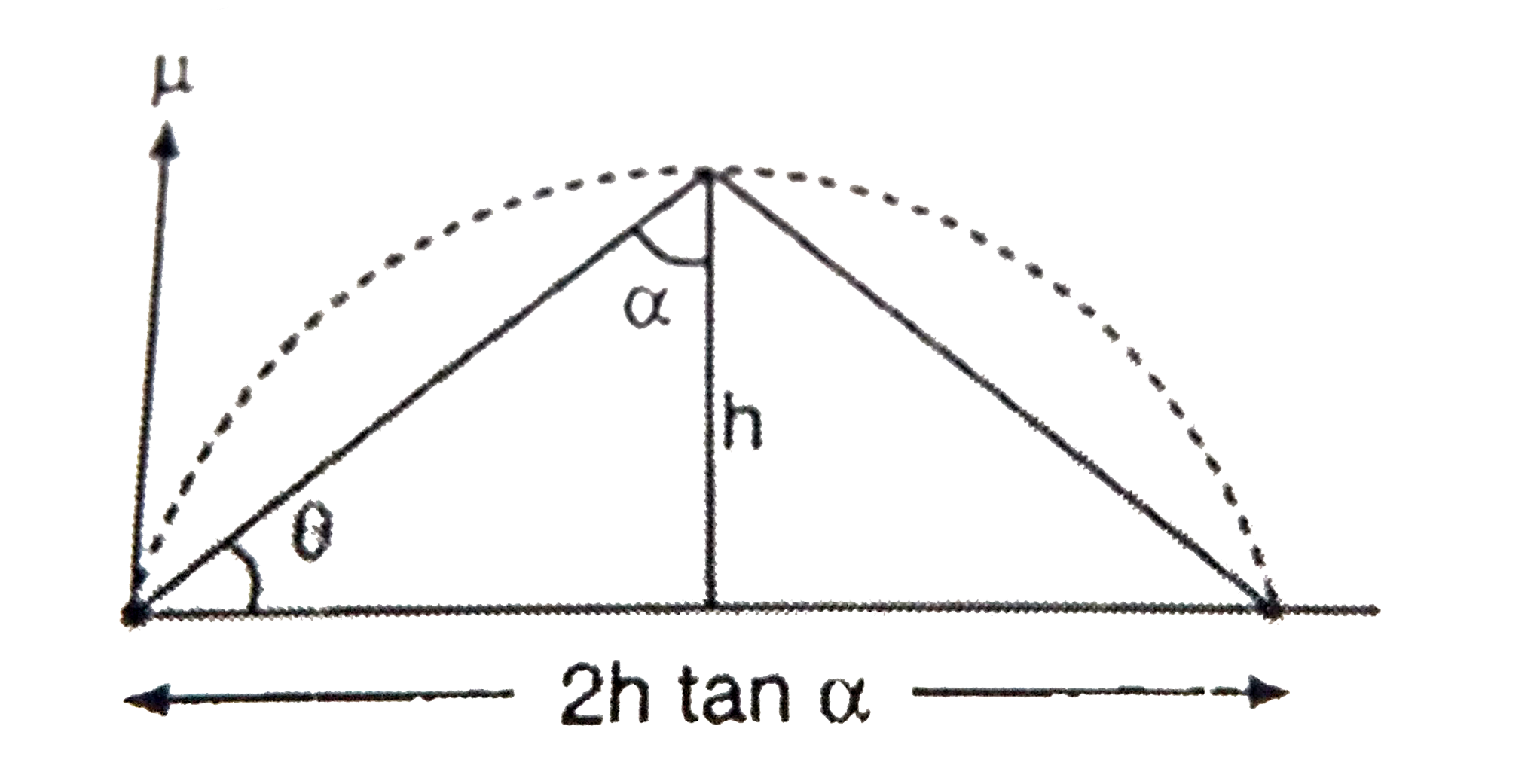
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If $α and β$ be the base angles and $θ$ the angle of projection, prove that $tan θ = tan α + tan β$ .

Video Solution

Answer

Step by step video & image solution for A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If alpha and beta be the base angles and theta the angle of projection, prove that tan theta = tan alpha + tan beta . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Knowledge Check

A particle is thrown over a triangle from one end of horizontal base and grazing over the vertex falls on the other end of the base. If $α, β$ are the base angles and $θ$ the angle of projection, then
A $tan θ = tan α - tan β$
B $tan θ = tan β - tan α$
C $tan θ = tan α + tan β$
DNone of these
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If $30^{\circ} and 60^{\circ}$ be the base angles and $θ$ the angle of projection then $tan θ$ is
A $\frac{2}{\sqrt{3}}$
B $\frac{4}{\sqrt{3}}$
C $\frac{1}{3}$
D3
If a $cos 2 θ + b sin 2 θ = c$ has $α and β$ as its solution, then the value of $tan α + tan β$ is
A $\frac{c + a}{2 b}$
B $\frac{2 b}{c + a}$
C $\frac{c - a}{2 b}$
D $\frac{b}{c + a}$

PHYSICS GALAXY - ASHISH ARORA-KINEMATICS-Unsolved Numerical Pro.

Home
Ask Doubt
Profile

A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .

Topper's Solved these Questions

Similar Questions

Knowledge Check

A particle is thrown over a triangle from one end of horizontal base and grazing over the vertex falls on the other end of the base. If α,β are the base angles and θ the angle of projection, then

A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If 30∘and60∘ be the base angles and θ the angle of projection then tanθ is

If a cos2θ+bsin2θ=c has αandβ as its solution, then the value of tanα+tanβ is

PHYSICS GALAXY - ASHISH ARORA-KINEMATICS-Unsolved Numerical Pro.

A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If $α and β$ be the base angles and $θ$ the angle of projection, prove that $tan θ = tan α + tan β$ .

A particle is thrown over a triangle from one end of horizontal base and grazing over the vertex falls on the other end of the base. If $α, β$ are the base angles and $θ$ the angle of projection, then

A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If $30^{\circ} and 60^{\circ}$ be the base angles and $θ$ the angle of projection then $tan θ$ is

If a $cos 2 θ + b sin 2 θ = c$ has $α and β$ as its solution, then the value of $tan α + tan β$ is