A particle is thrown such that its time of flight is 10s and horizontal range is 500m.
(i) Hmax=125m
(ii) u=50√2m/s
(iii) θ=45∘
(iv) velocity at highest point =50m/s
(i), (ii), (iii)
(ii), (iii), (iv)
(i), (ii), (iv)
all option are correct
The correct Answer is:D
T=2usinθg=10⇒usinθ=50
R=ucosθT⇒500=ucosθ×10⇒ucosθ=50
(i) Hmax=u2sin2θ2g=(50)22×10=125m
(ii) u=√(usinθ)2+(ucosθ)2=50√2m/s
(iii) tanθ=usinθusinθ=1⇒θ=45∘
(iv) velocity at highest point =ucosθ=50m/s
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A projectile is projected with the initial velocity (6i+8j)m/s. The horizontal range is (g=10m/s2)
A96mB960mC9.6mD4.8m - Question 2 - Select One
The time of flight of a projectile is 10 s and range is 500m. Maximum height attained by it is [g=10m/s2]
A25mB50mC82mD125m - Question 3 - Select One
Range of a projectile with time of flight 10 s and maximum height 100 m is : (g=−10m/s2)
A200 mB125 mC100 mDData incoorect
A ball is thrown at an angle θ with the horizontal. Its time of flight is 2 s. Its horizontal range is 100 m. What is the horizontal component of velocity of projection ? Take g=10ms−2.
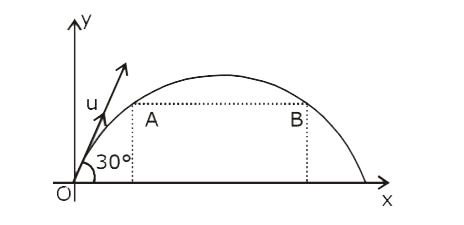
View SolutionA particle is thrown with a velocity of u m/s. It passes A and B as shown in figure at time t1 = 1 s and t2 = 3 s. The value of u is (g = 10 m/s2)
 View Solution
View SolutionA ball is thrown with a speed of 20 m s−1 at an elevation angle 45∘. Find its time of flight and the horizontal range ( take g = 10ms−2] lt
View SolutionA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
View SolutionA particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)View Solution

