A particle located at x=0 at time t=0, starts moving along with the positive x−direction with a velocity 'v' that varies as v=a√x. The displacement of the particle varies with time as
t2
t
t12
t3
The correct Answer is:A
To solve the problem, we need to find the displacement of a particle whose velocity varies with position as v=a√x.
1. Understanding the relationship between velocity and displacement:
The velocity v of the particle is given by:
v=a√x
We know that velocity is also defined as the rate of change of displacement with respect to time:
v=dxdt
Therefore, we can equate the two expressions:
dxdt=a√x
2. Separating variables:
Rearranging the equation gives us:
dx√x=adt
3. Integrating both sides:
We will integrate both sides. The left side requires the integral of 1√x and the right side is straightforward:
∫dx√x=∫adt
The integral of 1√x is 2√x, so we have:
2√x=at+C
where C is the constant of integration.
4. Applying initial conditions:
At t=0, the particle is at x=0. Plugging these values into the equation gives:
2√0=a(0)+C⟹C=0
Thus, our equation simplifies to:
2√x=at
5. Solving for x:
Now, we can solve for x:
√x=at2
Squaring both sides gives:
x=(at2)2=a2t24
6. Final Result:
Therefore, the displacement of the particle as a function of time is:
x(t)=a24t2
Summary:
The displacement of the particle varies with time as x(t)=a24t2.
---
The velocity v of the particle is given by:
v=a√x
We know that velocity is also defined as the rate of change of displacement with respect to time:
v=dxdt
Therefore, we can equate the two expressions:
dxdt=a√x
Rearranging the equation gives us:
dx√x=adt
We will integrate both sides. The left side requires the integral of 1√x and the right side is straightforward:
∫dx√x=∫adt
The integral of 1√x is 2√x, so we have:
2√x=at+C
where C is the constant of integration.
At t=0, the particle is at x=0. Plugging these values into the equation gives:
2√0=a(0)+C⟹C=0
Thus, our equation simplifies to:
2√x=at
Now, we can solve for x:
√x=at2
Squaring both sides gives:
x=(at2)2=a2t24
Therefore, the displacement of the particle as a function of time is:
x(t)=a24t2
The displacement of the particle varies with time as x(t)=a24t2.
Topper's Solved these Questions
Similar Questions
A particle located at "x=0" at time "t=0" starts moving along the positive "x" - direction with a velocity "v" that varies as "v=alpha sqrt(x)".The displacement "(x)" of the particle varies with time as "(alpha" is constant)
View SolutionA particle located at position x=0, at time t=0, starts moving along the positive x-direction with a velocity v2=αx (where alpha is a positive constant). The displacement of particle is proportional to
View Solution
Knowledge Check
A particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity that varies as v=p√x. The displacement of the particle varies with time as (where, p is constant)
At3Bt2CtDt1/2If the displacement of a particle varies with time as √x=t+3
Avelocity of the particle is inversely proportional to tBvelocity of particle varies linearly with tCvelocity of particle is proportional to √tDinitial velocity of the particle is zeroIf the displacement of a particle varies with time as √x=t+7 . The -
Avelocity of the particle is inversely proportional to tBvelocity of the particle is proportional to tCvelocity of the particle is proportional to √tDthe particle moves with a constant acceleration
The displacement to particle is zero at t=0andiszatt=t. It starts moving in the positive x-direction with a velocity which varies, v=k√x, wher (k) is a constant. Find the relation for variation of velocity with time.
View SolutionThe dispkacement of particle is zero at t=0 and it is x , at t−t. It starts moving in the positive x-direction with a velocity which varices as v=k√x, where (k) is a constant. Show that velocity is directly proprtional to time.
View SolutionIf the velocity "v" of a particle varies as the square of its displacement "x" then the acceleration varies as
View SolutionTwo particles 1 and 2 start simultaneously from origin and move along the positive X direction. Initial velocity of both particles is zero. The acceleration of the two particles depends on their displacement (x) as shown in fig.
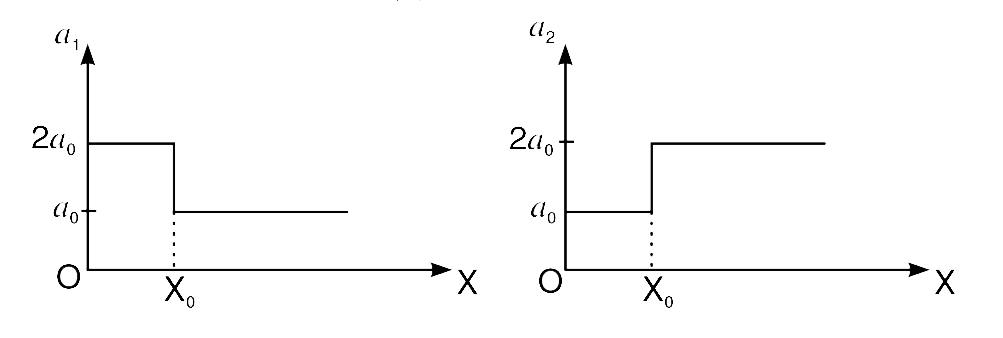
(a) Particles 1 and 2 take t1 and t2 time respectively for their displacement to become x0. Find t2t1.
(b) Which particle will cover 2x0 distance in least time? Which particle will cross the point x=2x0 with greater speed?
(c) The two particles have same speed at a certain time after the start. Calculate this common speed in terms of a0 and x0.
View Solution" If the velocity v of a particle varies as the square of its displacement "x" then the acceleration varies as "
View Solution
