Two stones are thrown up simultaneously from the edge of a cliff 240m high with initial speed of 10m/sand40m/s respectively . Which of the following graph best represents the time variation of relative position of the speed stone with respect to the first ?
( Assume stones do not rebound after hitting the groumd and neglect air resistance , take g=10m/s2)
( The figure are schematic and not drawn to scale )
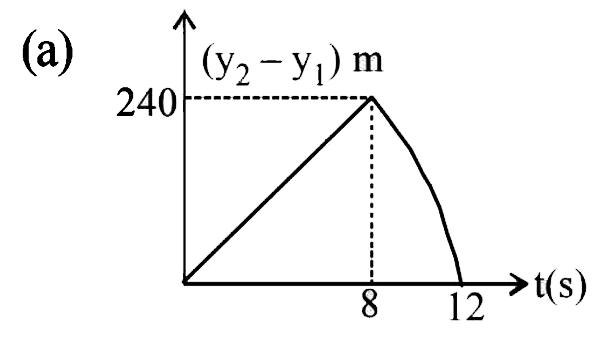
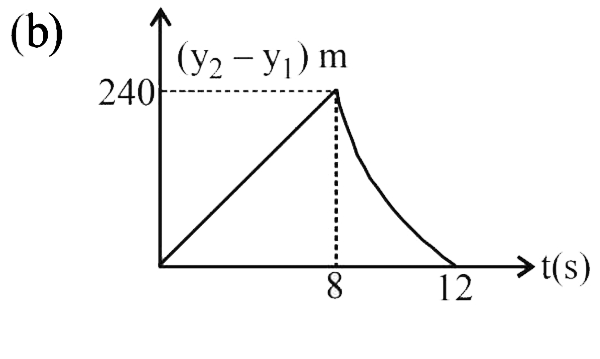
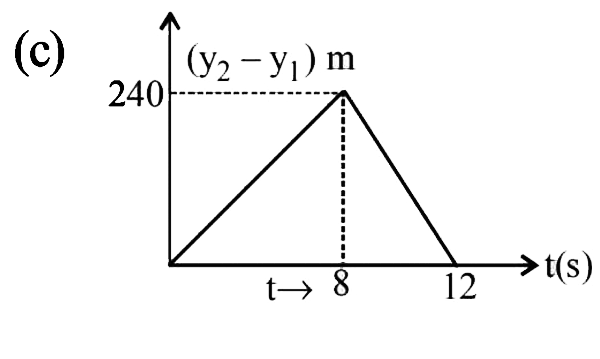
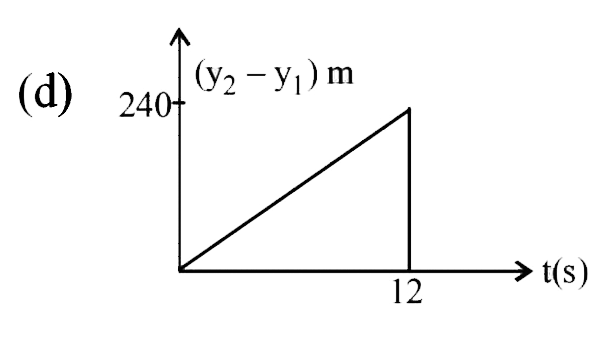
The correct Answer is:B
To solve the problem of two stones thrown from a cliff, we need to analyze their motion step by step.
Step 1: Understand the problem
We have two stones thrown from a height of 240 m. Stone A is thrown with an initial speed of 10 m/s, and Stone B is thrown with an initial speed of 40 m/s. We need to find the time variation of the relative position of Stone B with respect to Stone A.
Step 2: Calculate the time taken for each stone to reach the highest point
For Stone A (initial speed = 10 m/s):
- The time taken to reach the highest point (where final velocity = 0):
v=u−gt⟹0=10−10t⟹t=1 second
For Stone B (initial speed = 40 m/s):
- The time taken to reach the highest point:
v=u−gt⟹0=40−10t⟹t=4 seconds
Step 3: Calculate the maximum height reached by each stone
Using the formula for displacement:
s=ut+12at2
For Stone A:
sA=10×1+12(−10)(12)=10−5=5 m
For Stone B:
sB=40×4+12(−10)(42)=160−80=80 m
Step 4: Calculate the total height of each stone from the ground
The total height from the ground:
- Height of Stone A at its maximum:
HA=240+5=245 m
- Height of Stone B at its maximum:
HB=240+80=320 m
Step 5: Calculate the time taken for each stone to hit the ground
For Stone A (total time of flight):
- It goes up for 1 second and then comes down. The time to fall from 245 m:
s=ut+12gt2⟹0=245−12(10)t2⟹t2=49⟹t=7 seconds
Total time for Stone A = 1 second (up) + 7 seconds (down) = 8 seconds.
For Stone B (total time of flight):
- It goes up for 4 seconds and then comes down. The time to fall from 320 m:
s=ut+12gt2⟹0=320−12(10)t2⟹t2=64⟹t=8 seconds
Total time for Stone B = 4 seconds (up) + 8 seconds (down) = 12 seconds.
Step 6: Determine the relative position of Stone B with respect to Stone A
The relative position YB−YA can be calculated during their flight.
For t<1 (both stones are still rising):
YA=10t−5t2
YB=40t−5t2
YB−YA=(40t−5t2)−(10t−5t2)=30t
For 1<t<4 (Stone A is falling, Stone B is still rising):
YA=245−5(t−1)2
YB=40t−5t2
The relative position will change as Stone A falls.
For t>4 (Stone A is falling, Stone B is falling):
The relative position will be calculated based on their respective downward motions.
Step 7: Analyze the graphs
The graph representing the relative position will show a linear increase during the first second (when both are rising), a change in slope when Stone A starts falling, and then a parabolic shape as Stone B continues to fall after Stone A has hit the ground.
Conclusion
The graph that best represents the time variation of the relative position of Stone B with respect to Stone A will show a linear increase followed by a change in slope and then a parabolic curve after Stone A hits the ground.
We have two stones thrown from a height of 240 m. Stone A is thrown with an initial speed of 10 m/s, and Stone B is thrown with an initial speed of 40 m/s. We need to find the time variation of the relative position of Stone B with respect to Stone A.
For Stone A (initial speed = 10 m/s):
- The time taken to reach the highest point (where final velocity = 0):
v=u−gt⟹0=10−10t⟹t=1 second
- The time taken to reach the highest point:
v=u−gt⟹0=40−10t⟹t=4 seconds
Using the formula for displacement:
s=ut+12at2
sA=10×1+12(−10)(12)=10−5=5 m
sB=40×4+12(−10)(42)=160−80=80 m
The total height from the ground:
- Height of Stone A at its maximum:
HA=240+5=245 m
- Height of Stone B at its maximum:
HB=240+80=320 m
For Stone A (total time of flight):
- It goes up for 1 second and then comes down. The time to fall from 245 m:
s=ut+12gt2⟹0=245−12(10)t2⟹t2=49⟹t=7 seconds
Total time for Stone A = 1 second (up) + 7 seconds (down) = 8 seconds.
- It goes up for 4 seconds and then comes down. The time to fall from 320 m:
s=ut+12gt2⟹0=320−12(10)t2⟹t2=64⟹t=8 seconds
Total time for Stone B = 4 seconds (up) + 8 seconds (down) = 12 seconds.
The relative position YB−YA can be calculated during their flight.
YA=10t−5t2
YB=40t−5t2
YB−YA=(40t−5t2)−(10t−5t2)=30t
YA=245−5(t−1)2
YB=40t−5t2
The relative position will change as Stone A falls.
The relative position will be calculated based on their respective downward motions.
The graph representing the relative position will show a linear increase during the first second (when both are rising), a change in slope when Stone A starts falling, and then a parabolic shape as Stone B continues to fall after Stone A has hit the ground.
The graph that best represents the time variation of the relative position of Stone B with respect to Stone A will show a linear increase followed by a change in slope and then a parabolic curve after Stone A hits the ground.
Topper's Solved these Questions
Similar Questions
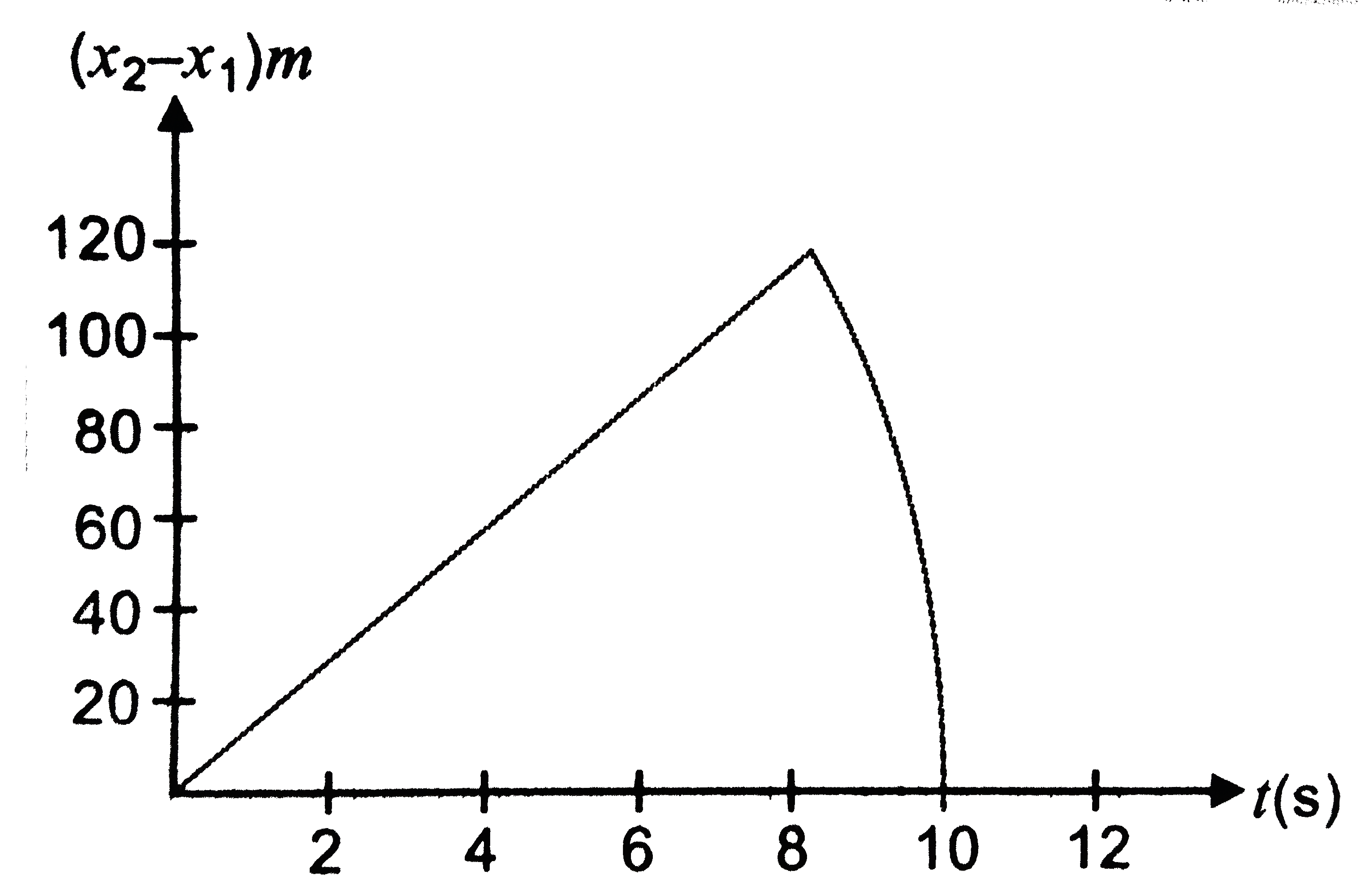
Two stones are thrown up simultaneously from the edge of a cliff 200m high with initial speeds of 15ms?−1 and 30−1. Verify that the graph shown in Fig. 2 ( NCT). 13 , correctly represents the time variation of the relativ e position of the second stone with respect to the first. Neglect the air resistance and assume that the stones do not rebound after hitting the ground. Taje g=10ms−2.Give equations for the linear and curved parts of the plot.
 .
.
View SolutionTwo balls are thrown up simultaneously from the top of a 400m high tower with speed 10m/s and 55m/s. Sketch a graph showing the separation between the balls versus time.
View Solution
Knowledge Check
Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
A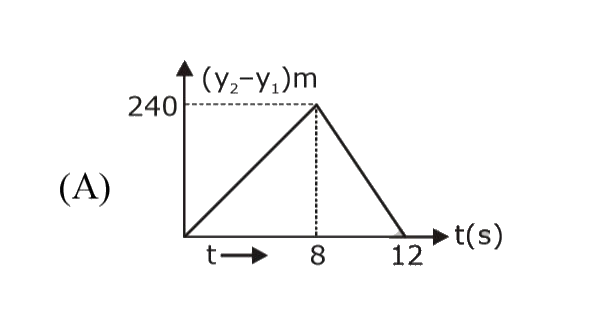 B
B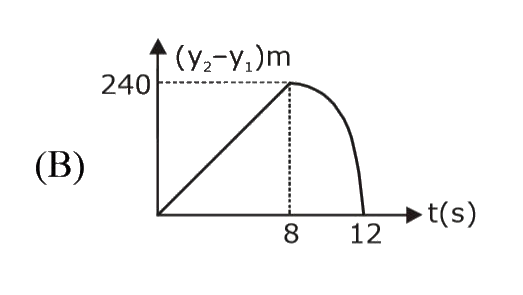 C
C D
D
Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
A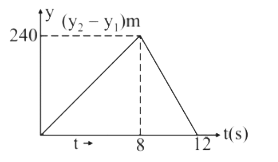 B
B C
C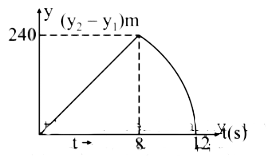 D
D
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15ms−1 and 30ms−1 respectively. The time variation of the relative position of the second stone will request to the first as shown in the figure. The equation of the linear part is
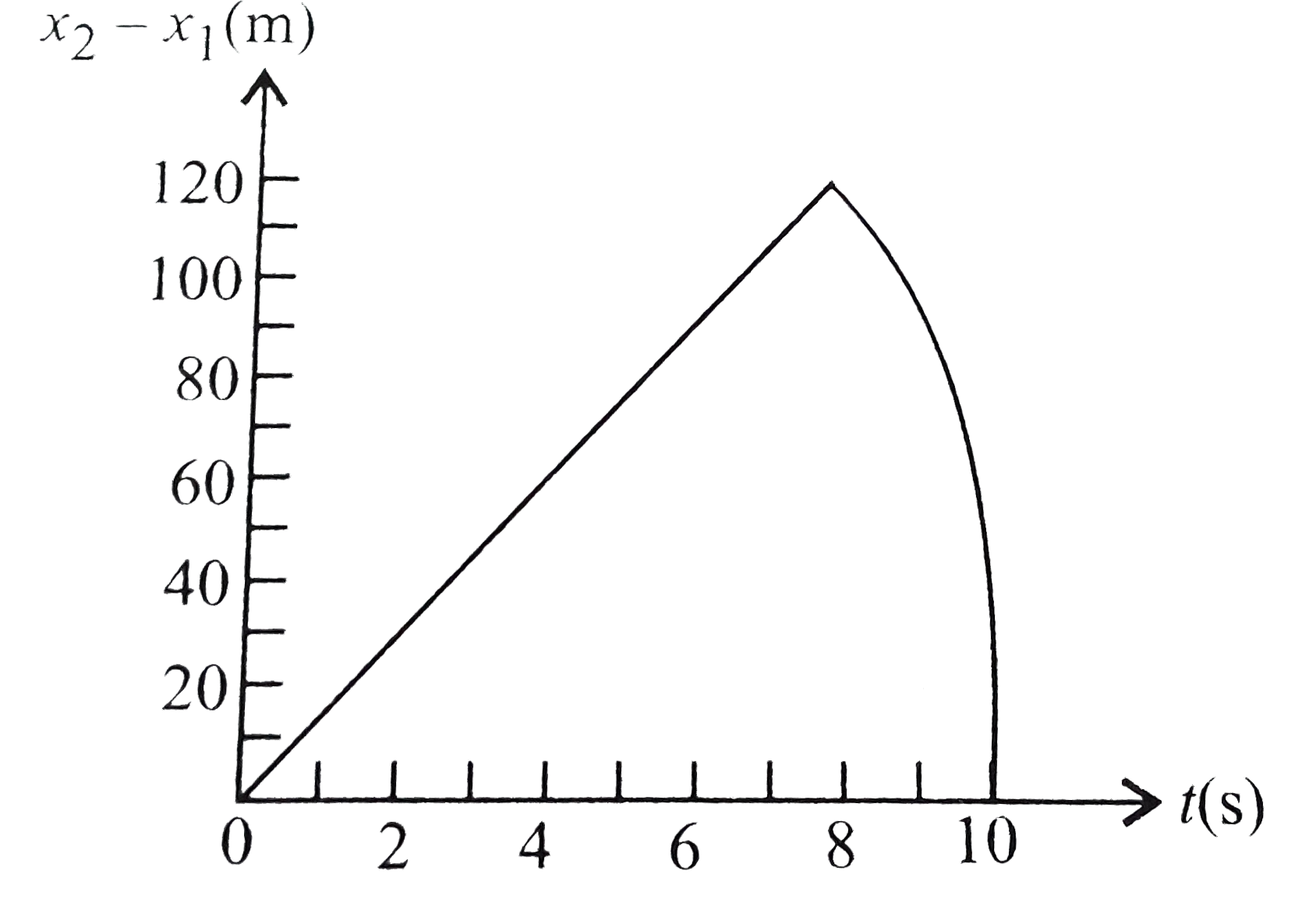 Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20t
Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20t
A stone is thrown upwards and it rises to a height 0f 200m. The relative velocity of the stone with respect to the earth will be maximum at :-
View SolutionTwo stones are thrown up simultaneously with initial speeds of u1 and u2(u2>1u1). They hit the ground after 6 s and 10 s respectively. Which graph in fig. correctly represents the time variation of Δx=(x2−x1) the relative position of the second stone with respect to the first upto t=10 s? Assume that the stones do not rebound after hitting the ground.
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff with initial speed vand2v. The relative position of the second stone with respect to first varies with time till both the stones strike the ground as.
View SolutionOne stone is projected horizontally from a 20m high cliff with an initial speed of 10ms−1. A second stone is simultaneously dropped from that cliff. Which of the following is true?
View SolutionOne stone is projected horizontally from a 20m high cliff with an initial speed of 10ms−1. A second stone is simultaneously dropped from that cliff. Which of the following is true?
View Solution
