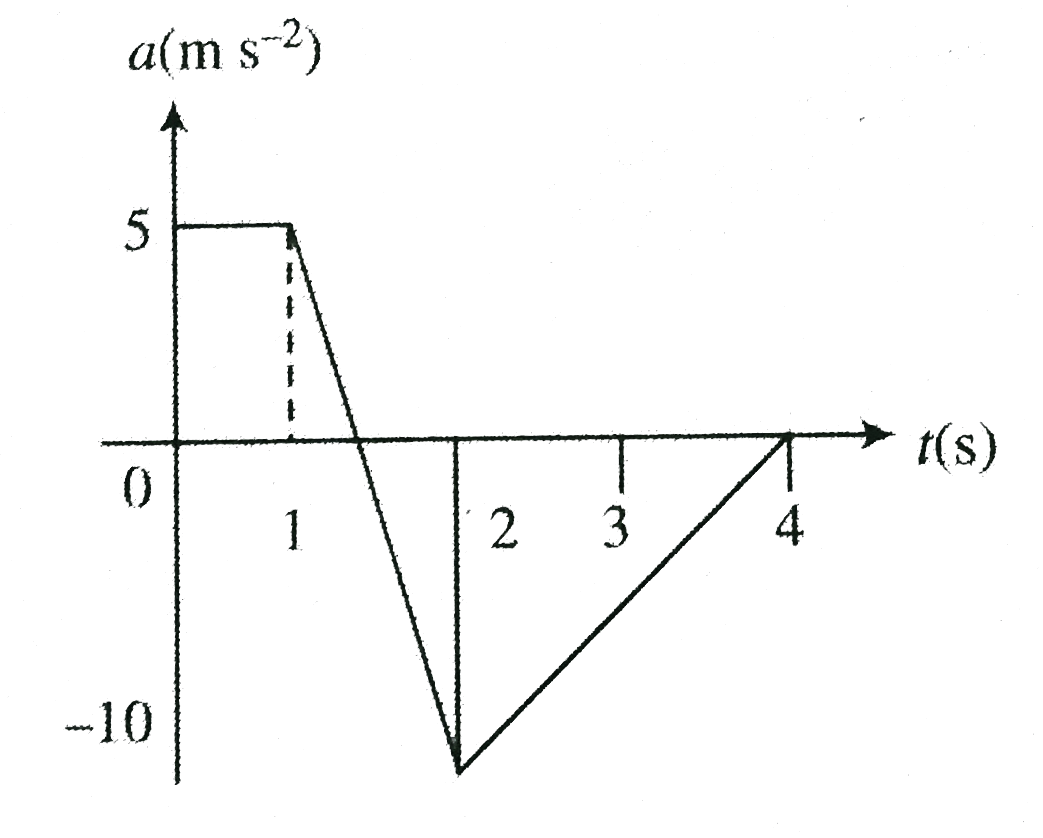
A particle moves aling x-axis with an initial speed v0=5ms−1. If its acceleration varies with with time asshown in a−t graph in .
 .
.
a. Find the time when the particle starts moving along - x direction
The velocity of the particle at t=4s can given as
→v4=→v0+Δ→v …(i)
where Δ→v≡A
(=area under a−t graaph during four seconds )
Referring to a−t graph , we have
A=A1+A2−A3−A4 ....(ii)
where A1=5×1=5,A2=12×x×5,
A3=12×(−1−x)×10, and A4=12×2×10=10
We can find x as following:
Using properties of similar triangles, we have x5=1−x10
This yields x=12.
 .
.
Substituting x=12∈A2=12×x×5
and A3=12(1−x)×10,
we have A2=−56 and A3=103.
Then substitution A1,A2,A3, and A4 in (ii), we have A=−7.5.
Negative area tells us that change in velcity is along −x direction
Δ→v=−7.5ms−1
Hence, substituting (i),
→v0=5ms−1 and Δ→v=−7.5ms−1,
we have
→v4=→v0+Δ→v=5−7.5=−2.5ms−1.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A particle moves vertically with an upwards initial speed v0=10.5ms−1. If its acceleration varies with time as shown in a-t graph in figure, find the velocity of the particles at t = 4s.

View SolutionThe position of a particle moving along x-axis varies eith time t as x=4t−t2+1. Find the time interval(s) during which the particle is moving along positive x-direction.
View SolutionThe fig. shows the v−t graph of a particle moving in straight line. Find the time when particle returns to the starting point.

View SolutionA particle starts moving in a circular path of radius R with an initial speed v0 clockwise. If the angular acceleration is αrad/s2 anticlockwise, the time when the acceleration and the velocity vectors of the particle become parallel, is
View SolutionA particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4−2t+t2. The speed of the particle will vary with time as
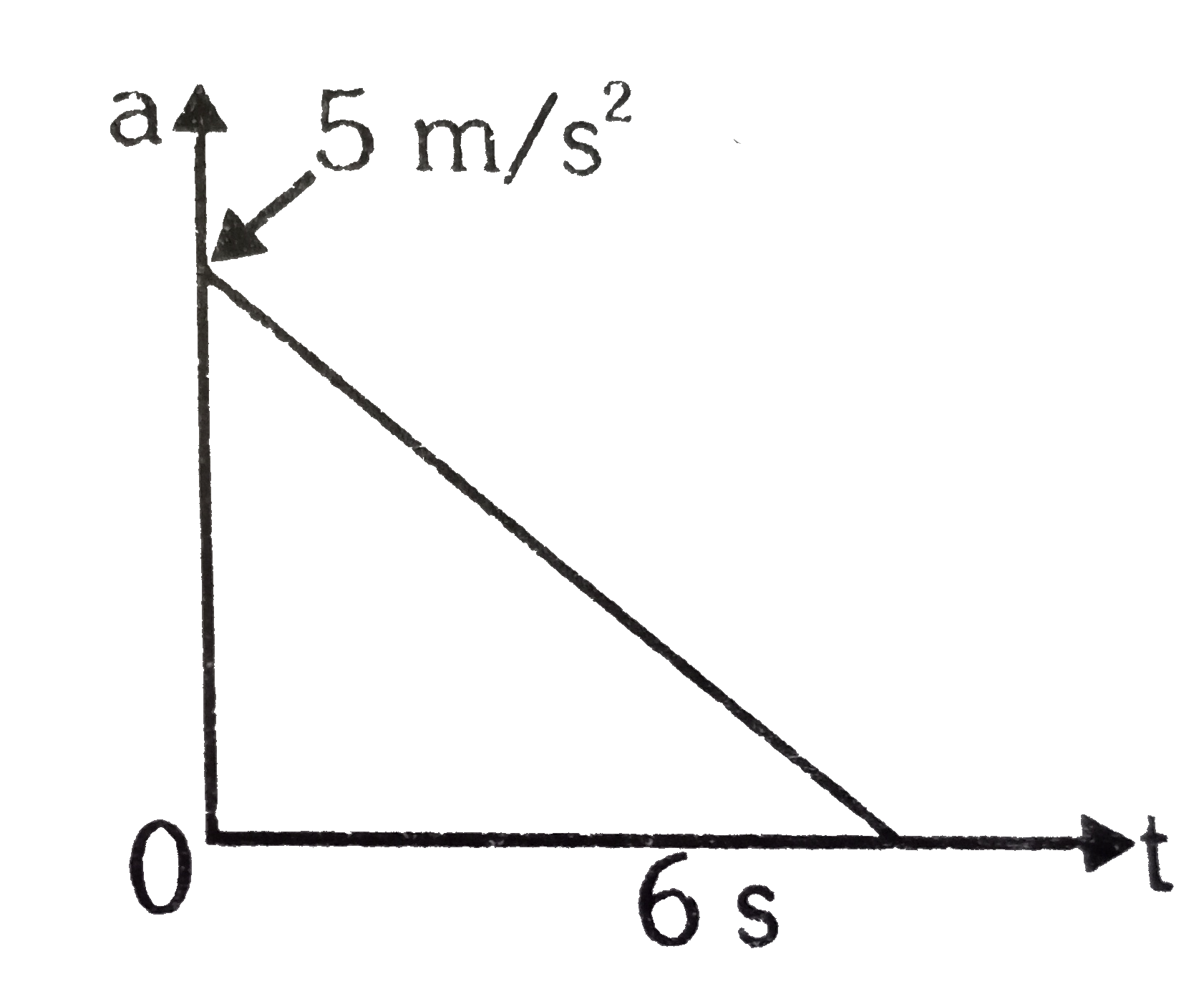
View SolutionA particle starts from rest. Its acceleration at time t=0 is 5m/s2 which varies with time as shown in the figure. The maximum speed of the particle will be
View SolutionA particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
View SolutionVelocity of particle moving along positive x-direction is v=(40−10t)m/s. Here,t is in seconds. At time t=0, tha x coordinate of particle is zero. Find the time when the particle is at a distance of 60 m from origin.
View SolutionA particle moves along x-axis such that its position veries with time as x=50t−5t2. Select the correct alternative (s).
View SolutionA particle move a distance x in time t according to equation x=(t+5)−1. The acceleration of particle is proportional to.
View Solution
