A particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4−2t+t2. The speed of the particle will vary with time as
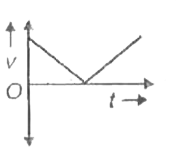

The correct Answer is:B
To solve the problem step by step, we need to analyze the motion of the particle given by the equation x=4−2t+t2.
Step 1: Differentiate the displacement function to find velocity
The velocity v(t) of the particle is the first derivative of the displacement x(t) with respect to time t.
v(t)=dxdt=ddt(4−2t+t2)
Step 2: Calculate the derivative
Now we differentiate each term:
- The derivative of 4 is 0.
- The derivative of −2t is −2.
- The derivative of t2 is 2t.
Putting it all together, we get:
v(t)=0−2+2t=2t−2
Step 3: Analyze the velocity function
The velocity function v(t)=2t−2 is a linear function of time t.
Step 4: Determine when the velocity is zero
To find when the particle changes direction, we set the velocity to zero:
2t−2=0
Solving for t:
2t=2⟹t=1
Step 5: Determine the sign of velocity
- For t<1, v(t)<0 (the particle is moving in the negative direction).
- For t=1, v(t)=0 (the particle is at rest).
- For t>1, v(t)>0 (the particle is moving in the positive direction).
Step 6: Determine the speed
Speed is the absolute value of velocity. Therefore, we can express speed s(t) as:
s(t)=|v(t)|=|2t−2|
Step 7: Write the piecewise function for speed
The speed can be expressed as a piecewise function:
s(t)={−(2t−2)if t<12t−2if t≥1
This means:
- For t<1, s(t)=2−2t
- For t≥1, s(t)=2t−2
Step 8: Graph the speed function
To graph the speed function:
- For t<1, the graph will be a decreasing line starting from s(0)=2 down to s(1)=0.
- For t≥1, the graph will be an increasing line starting from s(1)=0 and continuing upwards.
Conclusion
The speed of the particle varies with time as described by the piecewise function above, and the graph will reflect these changes in speed.
The velocity v(t) of the particle is the first derivative of the displacement x(t) with respect to time t.
Now we differentiate each term:
- The derivative of −2t is −2.
- The derivative of t2 is 2t.
The velocity function v(t)=2t−2 is a linear function of time t.
To find when the particle changes direction, we set the velocity to zero:
- For t<1, v(t)<0 (the particle is moving in the negative direction).
- For t=1, v(t)=0 (the particle is at rest).
- For t>1, v(t)>0 (the particle is moving in the positive direction).
Speed is the absolute value of velocity. Therefore, we can express speed s(t) as:
The speed can be expressed as a piecewise function:
- For t<1, s(t)=2−2t
- For t≥1, s(t)=2t−2
To graph the speed function:
- For t<1, the graph will be a decreasing line starting from s(0)=2 down to s(1)=0.
- For t≥1, the graph will be an increasing line starting from s(1)=0 and continuing upwards.
The speed of the particle varies with time as described by the piecewise function above, and the graph will reflect these changes in speed.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - B)
Explore 33 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - C)
Explore 36 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:EXERCISE
Explore 29 Videos
- MOTION IN A PLANEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A PLANEExercise:Assignement section -J (Aakash Challengers Questions)
Explore 7 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - J)
Explore 2 Videos
Similar Questions
A particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
View SolutionA particle moves along the x-axis in such a way that its x-co-ordinate varies with time as x=2–5t+6t2.
The initial velocity and acceleration of particle will respectively be-
View Solution
Knowledge Check
The co-ordinates of a moving particles at time t, given by x=at2,y=bt2. The speed of the particle is
A2(a+b)tB(a2+b2)1/2 tC2(a2+b2)1/2tD(a+b)t
A particle moves in an XY-plane in such a way that its x and y-coordinates vary with time according to
x(t)=t3−32t,y(t)=5t2+12
Find the acceleration of the particle, if t = 3 s.
View SolutionA particle moves in the x-y plane. It x and y coordinates vary with time t according to equations x=t2+2t and y=2t. Possible shape of path followed by the particle is
View SolutionA particle moves along x-axis such that its position veries with time as x=50t−5t2. Select the correct alternative (s).
View SolutionAn object moves along x-axis such that its position varies with time according to the relation x=50t−5t2
Here, x is in meters and time is in seconds. Find the displacement and distance travelled for the time interval t = 0 to t = 6 s.
View SolutionA particle moves along the X-axis as x=u(t−2s)=at(t−2)2.
View SolutionThe co-ordinates of a moving particle at any time t are given by x=ct2andy=bt2The speed of the particle is
View SolutionA particle moves along the X-axis as x=u(t−2s)+a(t−2s)2.
View Solution