A particle moves along ellipatical path gives by Calculate

A particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :

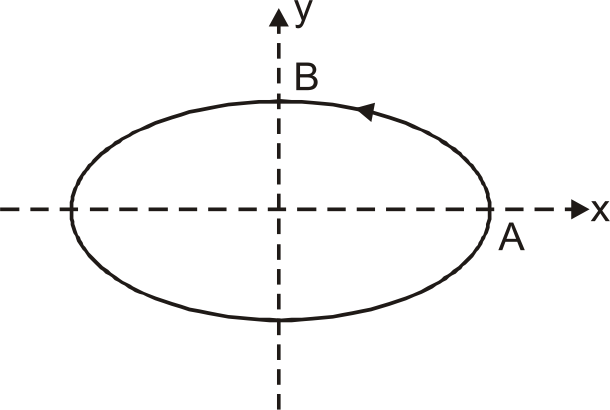AContinuously increases
Bcontinuously decreases
CRemains constant
Dfirst increases and then decreases
A particle is moving along an elliptical path with a constant speed. As it moves from A to B, magnitude of its acceleration:

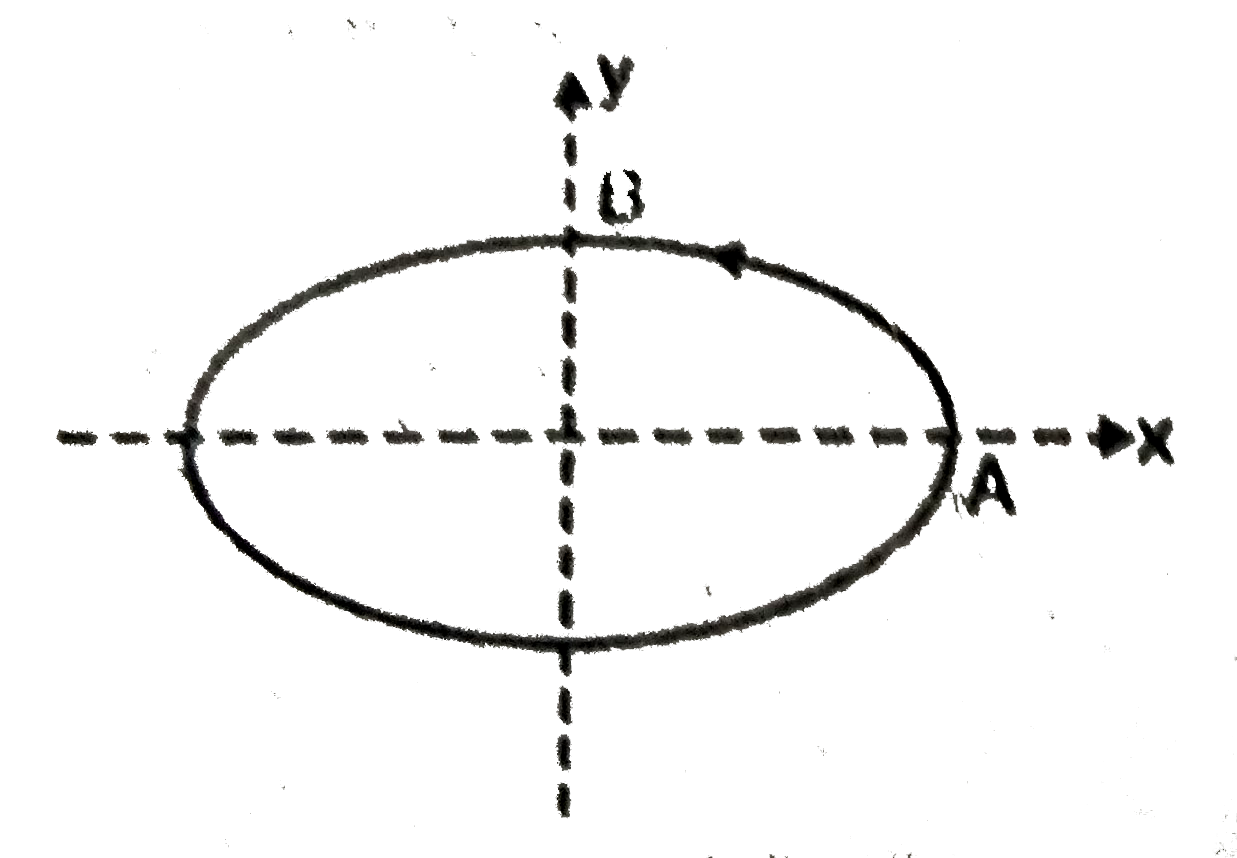AContinuously increases
Bcontinuoulsy decreases
Cremains constant
Dfirst increases and then decreases
A particle moves along the parabolic path $x = y^{2} + 2 y + 2$ in such a way that Y-component of velocity vector remains $5 m s^{- 1}$ during the motion. The magnitude of the acceleration of the particle is
A $50 m s^{- 2}$
B $100 m s^{- 2}$
C $10 (\sqrt{2}) m s^{- 2}$
D $0.1 m s^{- 2}$

A particle moves along ellipatical path gives by

Calculate (i) radial component of acceleration $({\to a}_{r})$
(ii) trasverse component of acceleration $({\to a}_{θ})$ .