A particle moves in the plane xy with constant acceleration 'a' directed along the negative y-axis. The equation of motion of the particle has the form y=px−qx2 where p and q are positive constants. Find the velocity of the particle at the origin of co-ordinates.
The correct Answer is:A, B, C
Comparing with,
y=xtanθ−gx22u2(1+tan2θ)
tanθ=b,g=a
and g2u2(1+tan2θ)=c
∴a(1+b2)2u2=c
∴u=u=√a(1+b2)2c
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Exercise 7.3
6 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Assertion And Reason
10 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Exercise 7.1
5 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionA particle moving along the X-axis executes simple harmonic motion, then the force acting on it is given by
where, A and K are positive constants.
View Solution
Knowledge Check
A particle moves in a plane with a constant acceleration in a direction different from the initial velocity. The path of the particle is
Astraight lineBarc of circleCparabolaDellipse
A particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
View SolutionThe equation of SHM of a particle is d2ydt2+ky=0, where k is a positive constant. The time period of motion is
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
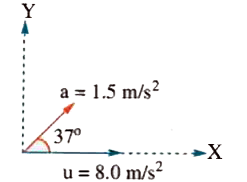
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View SolutionA particle moves in the XY-plane according to the law x=kt,y=kt(1−αt), where k and α are positive constants and t is time. The trajectory of the particle is
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionA particle moves in the x−y plane , accoding to the equation, r=(ˆi+2ˆj)Acosωt. The motion of the particle is
View Solution
