A particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

ax=(1.5ms2)(cos370)
=(1.5ms2)×45=1.2ms2
and a_y=(1.5 m/s^2)(sin37^0)<br>=(1.5 m/s^2) xx 3/5 = 0.90 m/s^2.<br>The∈itialvelocityhascompo≠nts<br>u_x=8.0 m/s<br>andu_y=0<br>At t=0, x=0 and y=-0<br>Thex−compo≠ntofthevelocityattimet=4.0sisgivenby<br>v_x=u_x+a_xt<br>=8.0 m/s+(1.2 m/s^2)(4.0s)<br>=8.0 m/s+4.8 m/s=12.8 m/s.<br>They−compo≠tofvelocityatt=4.0sigivenby<br>v_y=u_y+a_y t<br>=0+(0.90 m/s^2)(4.0s)=3.6 m/s<br>Thevelocityofthepartic≤∗t=4.0is<br>v=sqrt(v_x^2+v_y^2)= sqrt(12.8 m/s)^2 +(3.6 m/s)^2<br>=13.3 m/s.<br>Thevelocitymakesan∠θwiththeX−aξswhere<br>tantheta= (v_y)/(v_x) = (3.6 m/s)/(12.8 m/s) = 9/32<br>Thex−c∞rdiNAteatt=4.0sis<br> x= u_x t+1/2 a_x t^2<br>=(8.0 m/s)(4.0 s)+1/2 (1.2m/s^2)(4.0s)^2<br>=32m+9.6 m 41.6m.
The y=component at t=4.0 is
y=uyt+12at2
=12(0.90ms2)(4.0s)2
=7.2m
Thus, the particle is at (41.6 m, 7.2 m) at 4.0 s.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - worked out Examples20videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -113videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer14videos
PHYSICS AND MATHEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
Similar Questions
A particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
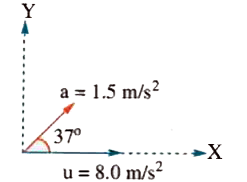
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
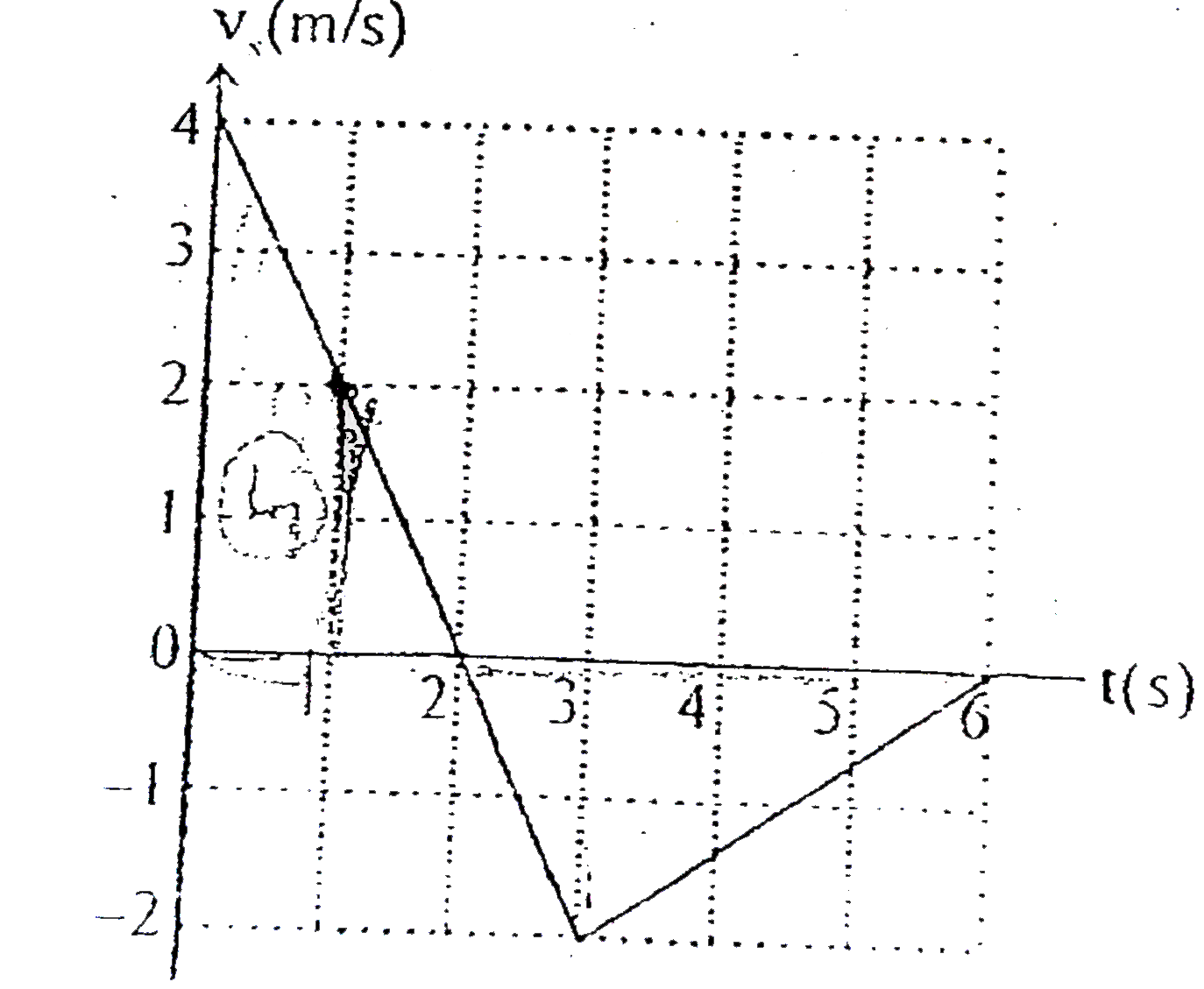 View Solution
View SolutionA time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionAcceleration of particle moving along the x-axis varies according to the law a=−2v, where a is in m/s2 and v is in m/s. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of time t.
(b) Find its position x as function of time t.
(c) Find its velocity v as function of its position coordinates.
(d) find the maximum distance it can go away from the origin.
(e) Will it reach the above-mentioned maximum distance?View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
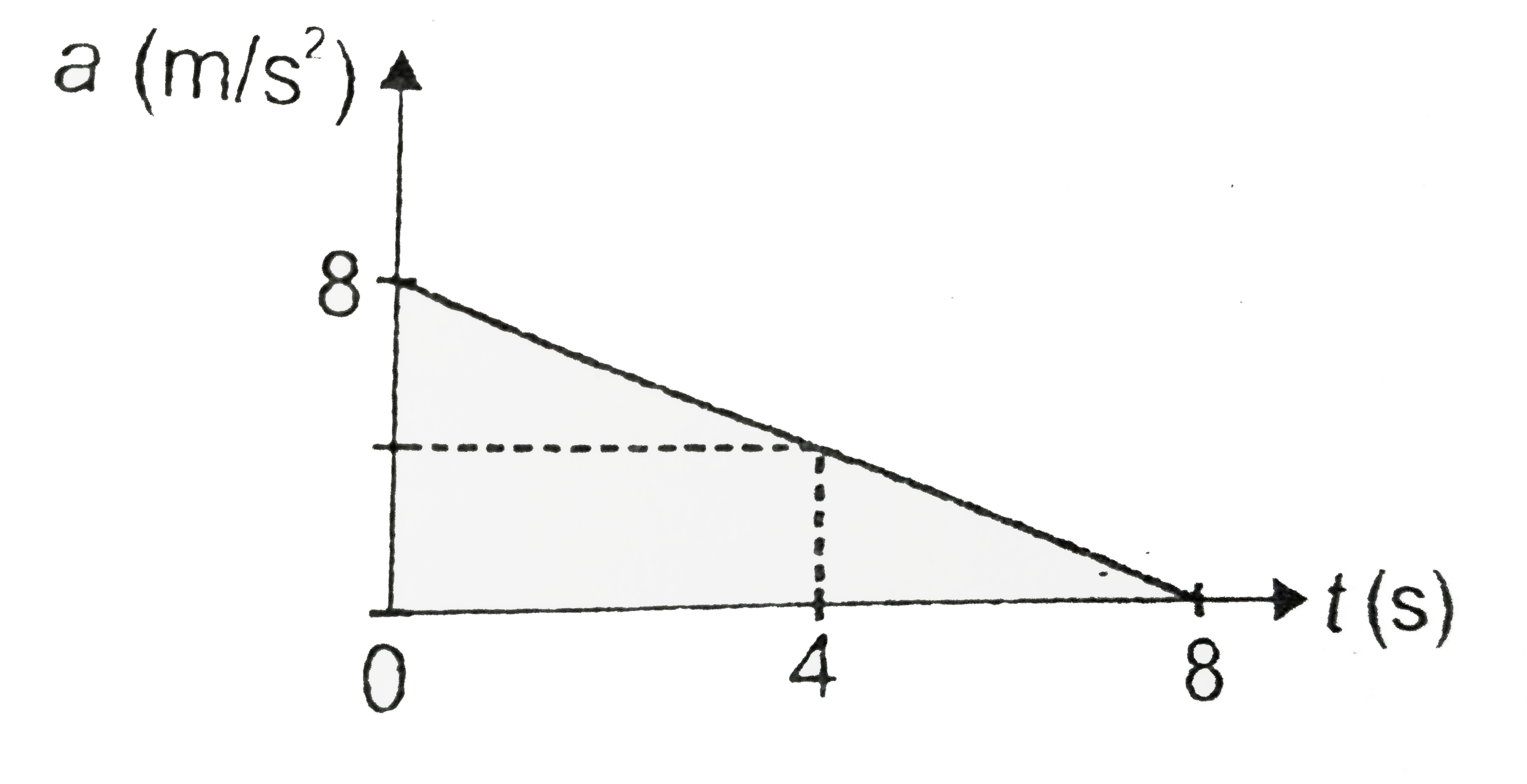 View Solution
View SolutionVelocity of a particle at time t=0 is 2ˆi m/s. A constant acceleration of 2ms2 acts on the particle for 2s at an angle of 60∘ with its initial velocity. Find the magnitude of velocity and displacement of particle at the end of t=2s.
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.View SolutionAt time t=0, a particle is at (2m,4m). It starts moving towards positive x-axis with constant acceleration 2m/s2 (initial velocity=0). After 2 s, an additional acceleration of 4m/s2 starts acting on the particle in negative y-direction also. Find after next 2 s.
(a) velocity and
(b) coordinates of particle.View Solution

