A particle of mass 0.2kg is moving in one dimension under a force that delivers constant power 0.5W to the particle.If the initial speed =0 then the final speed (in ms−1) after 5s is.
The correct Answer is:(5)
To solve the problem, we will follow these steps:
Step 1: Calculate the Work Done
The work done (W) by the force can be calculated using the formula:
W=P×t
where:
- P is the power delivered to the particle (0.5 W),
- t is the time duration (5 s).
Substituting the values:
W=0.5W×5s=2.5J
Step 2: Apply the Work-Energy Theorem
According to the work-energy theorem, the work done on the particle is equal to the change in kinetic energy (KE):
W=ΔKE
Since the initial speed is 0, the initial kinetic energy (KE_initial) is:
KEinitial=0
Thus, the final kinetic energy (KE_final) is:
KEfinal=W=2.5J
Step 3: Write the Kinetic Energy Formula
The kinetic energy of a particle is given by:
KE=12mv2
where:
- m is the mass of the particle (0.2 kg),
- v is the final speed we want to find.
Step 4: Set Up the Equation
From the previous steps, we have:
2.5J=12×0.2kg×v2
Step 5: Solve for Final Speed
Rearranging the equation to solve for v2:
2.5=0.1v2
v2=2.50.1=25
Now, taking the square root to find v:
v=√25=5m/s
Final Answer
The final speed of the particle after 5 seconds is:
v=5m/s
---
The work done (W) by the force can be calculated using the formula:
W=P×t
where:
- P is the power delivered to the particle (0.5 W),
- t is the time duration (5 s).
W=0.5W×5s=2.5J
According to the work-energy theorem, the work done on the particle is equal to the change in kinetic energy (KE):
W=ΔKE
Since the initial speed is 0, the initial kinetic energy (KE_initial) is:
KEinitial=0
KEfinal=W=2.5J
The kinetic energy of a particle is given by:
KE=12mv2
where:
- m is the mass of the particle (0.2 kg),
- v is the final speed we want to find.
From the previous steps, we have:
2.5J=12×0.2kg×v2
Rearranging the equation to solve for v2:
2.5=0.1v2
v2=2.50.1=25
v=√25=5m/s
The final speed of the particle after 5 seconds is:
v=5m/s
Topper's Solved these Questions
Similar Questions
A particie of mass 10 kg is driven by a machine that delivers a constant power of 20 watts. If particle starts from rest and moves along a straight line, then force (in Newton) on particle at time t(t> 0) is
View SolutionA body of mass m = 1 kg is moving in a medium and experiences a frictional force F = -kv, where v is the speed of the body. The initial speed is v0=10ms−1 and after 10 s, its energy becomes half of the initial energy. Then, the value of k is
View SolutionA particle of mass 2 kg is moving in circular path with constant speed 20 m/s. The magnitude of change in velocity when particle travels from A to P will be
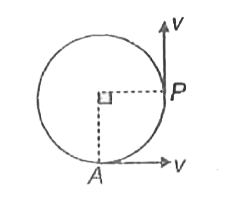
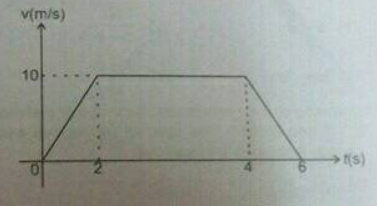
View SolutionA particle of mass 1 kg is moved under the action of a force and velocity time graph of the particle is shown in figure.Work done by the force from t=0 to t=6 s Is
View SolutionThe displacement 'x' (in meter) of a particle of mass 'm' (in kg) moving in one dimension under the action of a force is released to time 't' (in sec) by t2=√x+2. The displacement of the particle when its velocity is zero will be.
View SolutionA body of mass 10 kg is being acted upon by a force 3t2 and an opposing constant force of 32 N. The initial speed is 10ms−1.The velocity of body after 5 s is
View SolutionA particle of mass 0.2 kg exectites SHM under a force of F = - 20x N. If speed of particle at mean position is 12 m/s then the amplitude of oscillations is
View SolutionA particle of mass m, moving in a circle of radius R, has a velocity v=v0(1−e−γt) The power delivered to tha particle by the force at t=0 is
View SolutionA particle of mass 1031kg is moving with a velocity equal to 105ms−1. The wavelength of the particle is equal to
View SolutionA particle is kept at rest at the origin. A constant force →F starts acting on it at t=0. Find the speed of the particle at time t.
View Solution
