A particle of mass 0.50 kg executes a simple harmonic motion under a force F=−(50Nm−1)x. If it crosses the centre of oscillation with a speed of 10ms−1, find the amplitude of the motion.
The kinetic energy of the pasrticle when it is at the centre of oscillation si E=12mv2
=12(0.50kg)(10ms−1)2
=25J
The potential energy is zero here. At the maximum displacement x=A, the speed is zero and hence the kinetic energy is zero. The potential energyi here is 12kA. As there is no loss of energy.
=12kA2=25J .............i
The force on the particle is given by
F=(50Nm−1)mx.
Thus the spring constant is k=50Nm−1 Equation i gives
=12(50Nm−1)A2=25J
o A=1m
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Worked Out Examples
22 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Short Answer
13 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A particle of mass 0.50 kg executes a simple harmonic motion under a force F = – (50 N/m)x. If it crosses the centre of oscillation with a speed of 10 m/s, find the amplitude of the motion.
View SolutionA particle of mass 0.50kg executes a simple harmonic motion under a forve F=−(50n/m)x. If crosses the centre of oscillation with a speed of 10m/s, find the amplitude of the motion.
View Solution
Knowledge Check
A particle of mass 0.1 kg executes SHM under a for F=(−10x) N. Speed of particle at mean position 6m/s. Then amplitude of oscillations is
A0.6 mB0.2mC0.4mD0.1mA body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
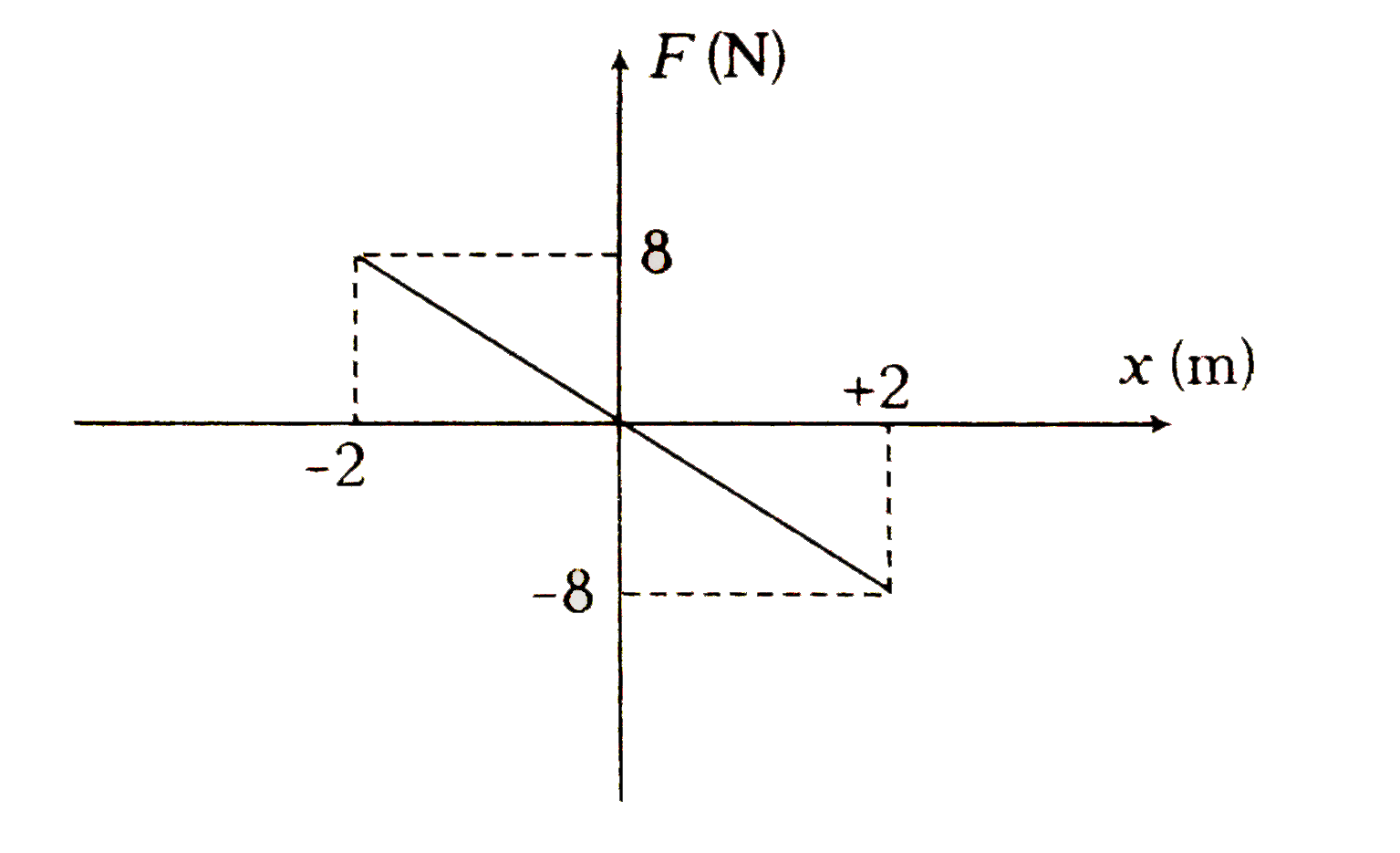 A1.05 sB0.52 sC0.25 sD0.31 s
A1.05 sB0.52 sC0.25 sD0.31 sA particle executing simple harmonic motion of amplitude 5cm has maximum speed of 3.14cm/s. The frequency of its oscillation is
A3HzB2HzC4HzD1Hz
A particle of mass 40 g executes a simple harmonic motion of amplitude 2.0 cm. If the time period is 0.20 s, find the total mechanical energy of the system.
View SolutionA particle of mass 0.2 kg executes SHM under a force of F = - 20x N. If speed of particle at mean position is 12 m/s then the amplitude of oscillations is
View SolutionA body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
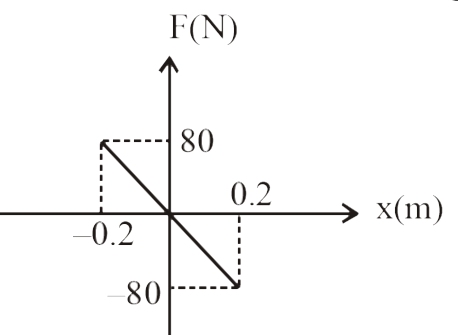
View SolutionA particle is executing simple harmonic motion of amplitude 9 m. At what point the speed of the particle will be one third of its maximum speed ?
View SolutionA particle executing simple harmonic motion of amplitude 5 cm has maximum speed of 31.4 cm / s . The frequency of its oscillation is
View Solution
